Johan Dubbeldam, Ph.D.
I am a mathematical physicist working in the fields of dynamical systems and
statistical physics. I am particularly interested in so-called translocation
of long polymers through nanopores, a phenomenon whose dynamics is governed
by stochastic processes.
Currently I am an associate
professor in the Delft Institute of Applied Mathematics (DIAM) and I
work in the divison "Mathematical Physics" headed by prof. Heemink.
After receiving my master's degree from Utrecht University and my Ph.D. from the Free University University of Amsterdam, I held
postdoctoral research positions at the Eindhoven University of Technology and
the Max Planck Institute in Mainz. Since 2006 I have been affiliated with
Delft University of Technology, where I have continued my work on translocation,
polymer models, nonequilibrium statistical physics, mathematical biology and dynamical systems.
A Ph.D. student that I have supervised, M.A.K. Bulelzai , has successfully defended his
thesis in January 2014 on the dynamics
of processes involved in atherosclerosis. Another PhD student, defending his thesis in June 2018, Kaihua Xi, has investigated the
stability of electric power grids using a complex network perspective. This work ties in nicely with my new interest
on complex networks.
More details about my work can be found by clicking on the links that can be found in the menu on your left.
Translocation, non-equilibrium statistical physics and fractional Brownian Motion
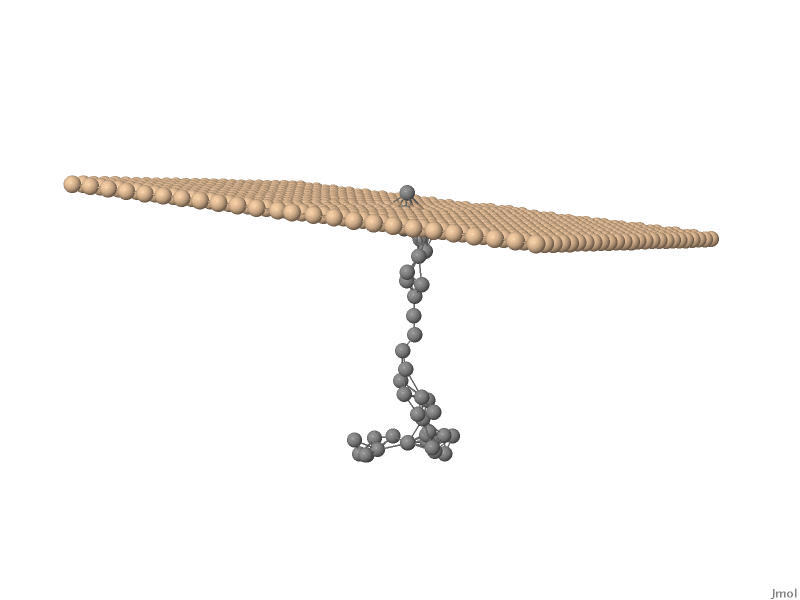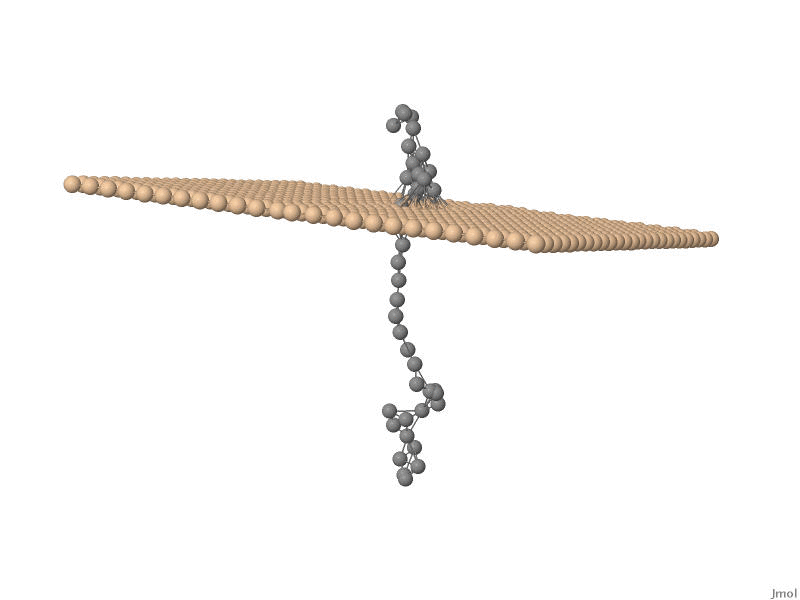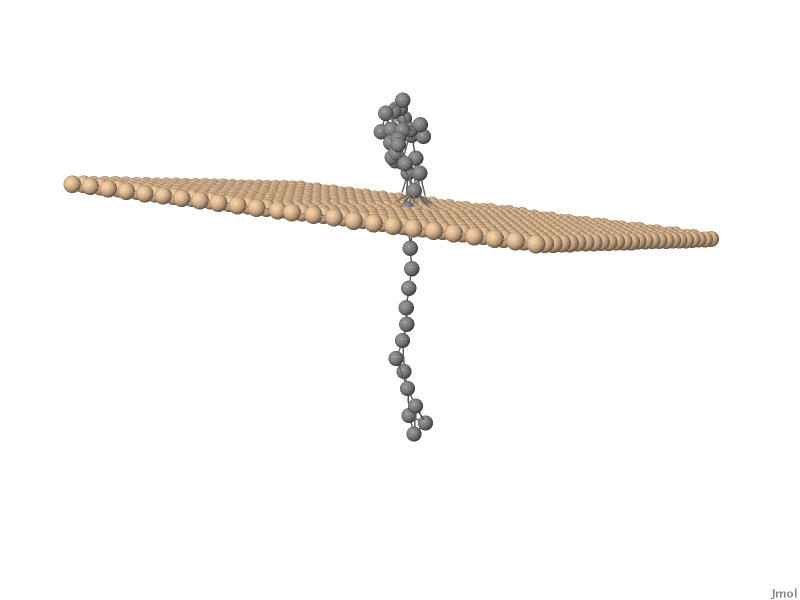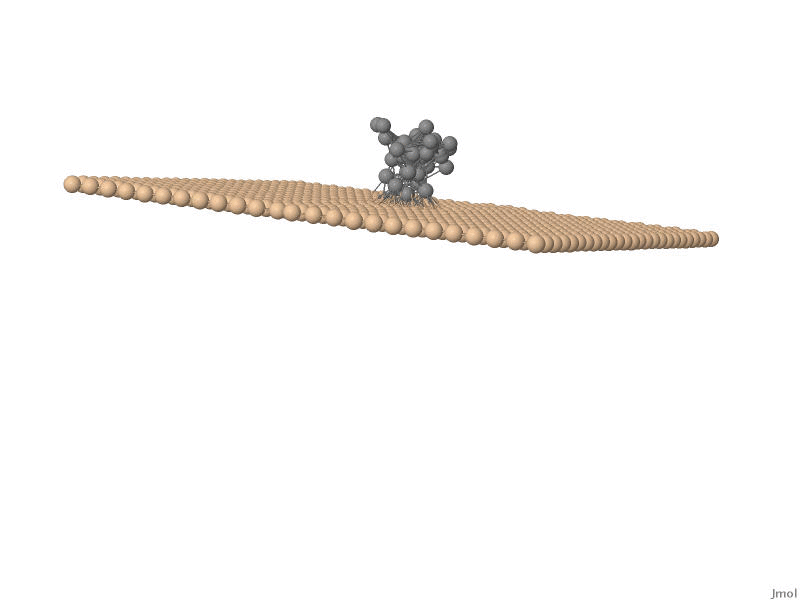One of the major branches in theoretical physics is non-equilibrium statistical
physics. This field has been greatly influenced by the work of Kubo, Priogine,
and Haken among others. Nowadays different biological processes are studied using
methods from non-equilibrium statistical physics. A particularly interesting phenomena is the
stochastic movement of a polymer chain, such as for example DNA, through nanosized pores. This
physical process, mostly referred to as translocation , has huge
potential applications in, for example, DNA sequencing and protein transport accross cell membranes.
Enormous experimental has been achieved recently. The bionanoscience group of prof. Cees Dekker
at the Kavli institute at TUDelft has made important contributions to these recent advances.
In collaboration
with my colleagues, V. Rostiasvili, A. Milchev and T. Vilgis from the
Max-Planck Institute in Mainz
new models for translocation process are developed using both numerical and analytical methods. We found
a strong negative velocity auto-correlation for the bead inside the pore. In fact, detailed knowledge
of the velocity-autocorrelation would facilitate a description in terms of a fractional Fokker-Planck equation.
Complexity, dynamical systems and networks
Besides translocation I am interested in dynamical systems in general and the dynamics of networks
in particular. A host of applications have been found for the theory of complex systems, random graphs and
(stochastic) dynamics thereof, ranging from genetic networks to neuron networks. Daan Lenstra, Kirk Green and myself have
published an edited book about complexity and dynamical systems with Wiley publishers.
To find out more about this
and related stuff, please check out some of the links on this page.
Mathematical biology
Applications of mathematics to biological systems are plenty. Mathematical models help to shed light
on evolution theory and, more down to earth, help explain the functioning of particular systems inside an organism.
For example, the gradient sensing mechanism of a slime mold
Hope you enjoy this site!