To integrate our equations of motion by using discrete timesteps - whatever
of the three discussed simulation methods we're going to use - we always need
an algorithm to make it possible to approximate these equations in
our computer program.
There are today many different numerical integration methods, all with their
specific advantages and disadvantages, but many of their features can be described
in terms of the errors they introduce into the approximation if we compare them
with each other, using one fixed timeinterval and one fixed number of integration
steps.
With numerical integration techniques we always have to deal with to 2 major sources of error:
As said earlier, in my first (somewhat clumsy) multibody simulations I only used Euler and Runge-Kutta 4 for numerical integration. However, they both have some disadvantages : the first has a large discretisation error, so it requires a very small timestep to be accurate enough; the second has smaller discretisation errors, but takes a lot of computations per timestep which is why the round-off error grows much more rapid than with Euler.
It is important to notice that the acceleration (only) depends on the relative particle positions (which is always the case for a conservative force), so if we calculate the acceleration after an update of the positions,we actually use the approximated acceleration at time t+Dt and not at t !
Also, if we update the velocities before updating the positions we use the velocity at time t+Dt and not at t to find the new positions ! However, updating the positions before updating the velocities is no problem, as the velocities do not directly depend on the positions.
So, in a straight forward scheme the most logical order is:
| (1) | ||||||||||||||
| (2) | ||||||||||||||||||
| (3) | ||||||||||||||||||
| (4) | ||||||||||||||||||||
| (5) | ||||||||||||||
| (6) | ||||||||||||||
| (7) | ||||||||||||||
It is perfectly possible to use only positions and accelerations and completely forget about the speeds, by substituting the speed using the equation for the positions. But in that case we have to remember the previous positions (instead of the speed) to be able to integrate the second-order equation we'll then obtain.
For the Euler scheme in 1 this second order scheme looks like :
| (8) |
| (9) |
And for the Leapfrog scheme in 5 this yields in the same way :
| (10) |
The term s(t)-s(t-Dt) (which is the difference in position !) in fact represents the velocity term (now multiplied by Dt ) that we saw in the original equation schemes.
Discretisation errors are caused by the fact that by using an approximation
function to predict the new situation after one integration step, we will always
loose information if compared with the real situation. The size of the error
of course depends on the stepsize : the larger the step, the bigger the error.
But it also depends on the exact form of this approximation function : this is simply a straight line in the case of the Euler method (which is why we call it a first order method), but it is a parabola in the case of the Heun method (called a second-order method) and a 4th-order polynomial in the case of Runge-Kutta 4 (obviously called a fourth order method). In general we can say that the higher the order, the smaller the (discretisation) error.
What makes things worse is that the discretisation error is being propagated: the error made in step 1 will be amplified in step 2 and so on.
The local discretisation error (thus the error for one timestep) is given by the following general formula :
| (11) |
where r is the order of the integration method, F() is a function that gives the analytical solution of the differential equation and thus F(r)(xn) the value of the rth derivative of function F for step n , and e is the difference between the value we'll find at step n+1 using the numerical method and the exact functionvalue of x at step n+1 .
This looks rather horrible at first glance, but it is more easy to see this if we realize that basically every numerical approximation uses only the first few terms of the infinite Taylor series for F() to achieve the approximation :
| (12) |
Well, now we know the error made in one step, but of course we are more interested in the total discretisation error (this is the accumulated error after a number of steps) for a certain number of timesteps. Fortunately that looks a little easier:
For p = [(tn+p-tn)/(Dt)] timesteps the total discretisation error is roughly given by the formula :
| (13) |
with c being some unimportant constant and r the order of the integration method. The latter part of the equation was found by substituting the expression 11 for en+1 .
Note that the order of the global discretisation error is one lower than the order of the local discretisation error. Also, in particle simulation we may say in general that the global discretisation error can never be bounded for an unbounded number of timesteps, due to the nature of the problem.
More information about this subject can be found in many books about differential equations and numerical methods, such as in Boyce & Diprima ([]) : ``Numerical methods'', and Strauss ([]) : ``Computation of Solutions''.
Apart from discretisation errors, we also see a very different source of errors, introduced by the computer itself. Computers can almost never calculate exact answers: they are only accurate up to a limited number of digits, so every calculation introduces a round-off error. It is obvious that the more calculations we have to make in one timestep, the larger the maximum roundoff error for one timestep will be.
In some cases it is possible that the total round-off error will never exceed a certain maximum: in that case we will call the integration method stable.
In the case of our particle simulations several methods can be stable, provided the timestep is small enough. Stability often depends on the size of the timestep: if the timestep gets too large possibly stable systems will also become unstable.
Let's view the error-propagation for Euler and Leapfrog a little closer :
We can rearrange the Euler scheme to obtain a second-order difference equation, instead of two first order equations, simply by combining the two first order equations from the scheme into one equation, as already shown in 9. This equation could be rewritten to :
| (14) |
The round-off error at step n (called en ) is given by subtracting the approximation s¢n we found on the computer (using a limited number of digits) from the exact approximation sn (using an infinite number of digits) :
|
If we substitute this into 14 and bear in mind that the acceleration only depends on the positions we'll get :
|
Which is more or less equal to (approximating the second part using the standard definition for the derivative) :
|
Well, this is a standard second order difference equation. Assuming solutions of the form E = al1n+bln2 and substituting the term [(d a(sn-1))/(d sn-1)] with it's maximum amplitude WE2 , this yields us :
|
or (dividing by en and multiplying with l) :
|
This quadratic equation only has complex roots for 4-4*(1-(WEDt)2) < 0 or (WEDt)2 < 0 , which of course has no solutions. This implies that the error in the Euler scheme will at any rate be always nonperiodic, so unless both roots are smaller than 1 (in which case the error is being damped out) the Euler scheme will be always unstable.
Well, as both roots are only between ±1 for 1±[1/2]Ö{(WEDt)2} < 1 and because this equation obviously has no valid solutions for both roots at the same time, this must lead to the conclusion that Euler is in our case always unstable.
If we take the Leapfrog scheme from equation 10 we'll find in the same way as above :
| (15) |
|
Which is more or less equal to (approximating the second part using the definition for the derivative) :
|
This is again a standard second order difference equation. Let's assume again solutions of the form E = al1n+bln2 and also substitute the term [(d a(sn))/(d sn)] with it's maximum amplitude -WL2 , as we are only interested in this extreme. This yields us in the same way as with Euler :
|
or (dividing by en and multiplying with l) :
|
This quadratic equation has complex roots for ((WLDt)2-2)2-4 < 0 or (WLDt)4-4(WLDt)2 < 0 which equals to (WLDt)2((WLDt)2-4) < 0 . The first solution is trivial, the second yields to |WLDt| < 2 . As long as this is true the Leapfrog scheme will be stable, because the magnitude of the roots are in that case always on the unit-circle. Note that WLDt can't be negative, so there is no reason to investigate this any further.
For |WLDt| > 2 both roots are real and one of them is moving from -1 to -¥, while the other moves from -1 to 0 , so in this case we always have one root with a magnitude larger than 1 . Thus the Leapfrog scheme will be unstable for |WLDt| > 2 .
Of course this leaves us with the problem of finding WL , but for the moment it is enough that we know that under certain conditions this scheme is always stable with respect to the round-off error. Thus, how much it may look the same as Euler above it is definitely different at this point !!

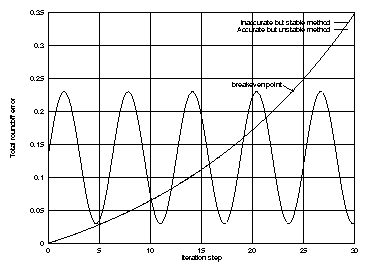
It is important to realize that short simulations may be better carried out with an unstable method that has a small roundoff error for the given interval, while for long simulations stability may be a far more important criterion than a small roundoff error over a certain interval. (see picture 1)
It is of course very important to be able to say something about how accurate a certain simulation run resembles the true situation. The best of course would be to have a system that could be solved analytically, so we could compare every value at every timestep with the correct value if we wish, but of course it would be pretty useless to carry out a simulation if we already knew the answer !
However, these kind of problems can be used as a kind of testcase for a certain program, before trying it on less trivial problems. What I often used was a system where a very light particle was running in a circle-shaped orbit around a very heavy particle at rest. Every deviation from the circle would be an indication of certain errors in the program.
What could be very useful too is to apply basic physical conservation laws on the simulation : at every time both the energy and the momentum in all directions should be conserved, so calculating these at a certain point in the simulation and compare them with their initial values may give a lot of information about the accuracy.
At every moment the total momentum of the system will be given by:
| (16) |
It is possible to only compare the amplitude of the total momentum as I did initially, but it is generally better to compare the momentum in every direction separately as this doesn't take any more time and memory. Due to a bug in the code I swapped the x and y components of the velocity in one case but wasn't able to notice it, as it had no influence on the amplitude of the total momentum ! It was only after this that I decided to compare the momentum in every direction separately ...
Higher order schemes have more problems in conserving momentum, but the nice thing about leapfrog and also wobble is that - although they are mathematically second order - they have the momentum conservation behaviour of a first order method !
But be careful: it is important to realize that - even if the total momentum is conserved - the individual momenta may still contain a large error ! However, fortunately enough this will often result in a large error in the total energy.
At every moment the total energy of the system will be given by the sum of the kinetic and potential energies. The potential energy is assumed to be zero at infinity and thus always negative, yielding us for a normal 3D system :
| (17) |
For a 2D system with genuine 2D forces such as we find for example in a 2D Particle-Mesh simulation (where the force drops ~ [1/r] instead of ~ [1/(r2)] ) the pairwise potential energy is proportional to log| ri® j| , resulting in a slightly diffferent formula :
| (18) |
In contrast with the momentum above the energy is much less likely being conserved :
Problems arise with the kinetic energy (the first part in both formulas) as it squares the speed, thus dropping the sign in the error, so that the cancellation that worked so nicely with the momentum doesn't work here anymore. Also the relative error is doubled by taking the square of the speed, which makes things even worse.
For the potential energy term (the second part in the formulas) there is also a problem : as it use the absolute value for the distance, the sign in the error is dropped here too, causing the same effect as with the kinetic energy above.
Note that the computation of the potential energy is an O(N2) operation. This implies that with large problems ( N > 104 ) this may take a relatively large amount of time, which is why I used an approximation for this value in the case of the analyser program described in chapter .
Furthermore the discretisation error often causes the system to slowly heat up, for reasons not shown in this report. This also contributes to an increasing deviation from the initial energy. Some algorithms solve this heating problem by decreasing the per-particle energy after a certain number of timesteps with a small factor, but as I consider this a very inelegant solution I did not implement this.
So, in general we may say that energy is not conserved, whatever scheme we use. On the other hand, if the deviation is not to large, the simulation may still be quite accurate. Deviations as large as 1-5 % are no problem in many cases.
It is obvious that a force that drops with the seventh power of the distance will be far less important for far away particles, than a force that drops only with the square of the distance, like i.e. a gravitational force. In fact the influence of the first one may be completely ignored for all particles except for the ``nearest neighbours'', while the second may still be felt at a considerably longer distance.
So, we see that the distance over which the force can influence other particles can differ very widely. A force that is only felt at close locations could make it possible to use a much faster algorithm by totally neglecting the force at distances higher than a certain threshold. Such a force will be called a short range force from now on. On the other hand a force could work over a very long distance and this one is obviously called long range force.
Special attention should be paid to the density: even if a force drops sharp with the distance it couldn't be neglected if the number of far away particles is much higher than the number of close particles, although it can be possible in some cases to only take into account the total influence of many far away particles, as we do in Tree-code simulations.
Special problems concerning a (more or less) uniform density in 2D and 3D space will be discussed hereafter :
Consider a system of particles with a uniform density for the moment. This means that the concentration of particles is more or less the same over the whole working area.
Note: In a purely uniform distribution all contributions will cancel out each other, as for every force contribution from a certain distance there is another contribution from exact the opposite side, effectively cancelling the first one. So only for places where the distribution is not purely random the discussion hereafter will hold completely (i.e. near the edges), although what it says about each individual force contribution will always be true, although not very useful.
Now let's see what happens to the total force from all particles at a given distance on a certain test particle, if we assume that the force drops with the square of the distance (as is the case with the 3D gravitational force) both for a 2D system and a 3D system.
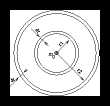
| (19) |
| (20) |
| (21) |
| |||||||||||||||
| |||||||||||||||||||
| (22) |
| (23) |
| (24) |
| (25) |
It is obvious that with forces that drop more progressively than [1/(r2)] forces, the faraway particles can be again safely neglected and it is equally obvious that in simulations with a higher dimension than 3 (whatever it may stand for !) also these more progressive forces sometimes can't be ignored anymore.
The exact size of the timestep determines the amount of ``linearisation'' introduced by the numerical integration if compared with the real problem. Of course this shouldn't be too far off from reality. On the other hand: the larger the timestep, the less calculations we need and thus the faster our simulation will be. What we should ask ourselves is how large can we make it without causing serious problems ?
It is obvious that for a particle with a constant speed and no forces working on it we can make our timestep as large as we like. So, the amount of change in speed within one timestep determines how accurate our approach will be : i.e. if the speed doubles within one timestep the results will be very unreliable.
From this follows that we shouldn't allow the speed to change more than about 5-10 % in one timestep. But, this is impossible for a particle initially at rest ! To avoid this problem we'd better use an absolute maximum than a relative maximum. We could i.e. look at the average initial speeds and choose the maximum allowable change according to this average.
Also important is the change in the angle or direction: if the magnitude of the speed hasn't changed it is still possible that the direction has changed considerably. Of course we have the same problem here as above: for a particle initially at rest it is impossible to say something about the relative change in direction.
The easiest thing is to look at the absolute change of speed in each separate direction: in that case we will cover both the magnitude and the direction criteria.
Another aspect in choosing the timestep is the closest distance between 2 particles that we allow (the COLLISIONDETECT macro in the code). If the speed is so large that in one timestep a particle has moved more than the collision detect distance, there could have been a collision between 2 particles without any detection, causing the new positions to be meaningless ! This is even a bigger problem in the case of our gravitational or Coulomb forces: the interparticle force goes to ¥ if the particle distance goes to 0 !
So we never should allow the position to change with more than about 10-25 % of the collision detect distance.
It may be a good idea to relate the collision detect distance to the maximum allowable acceleration: i.e. 2-5 times as large, rather than make it a fixed value that could be only changed at compile time.
Another important restriction for the choice of the timestep was already given earlier in this chapter: it should be small enough to avoid round-off errors to become unbounded.
If we use an algorithm where the interparticle distance doesn't play a direct role in the computation of the acceleration -such as is the case with the Particle-Mesh method - a minimum collision distance will be meaningless.
However, the Particle-Mesh method has another limit instead: it should never be possible that a particle moves with more than 10-25 % of the mesh distance. This immediately brings us to another problem: if we halve the mesh distance, we should also halve the timestep !
In the discussion above we simply stop the simulation if one of the limits is being exceeded. Another possibility could be to make the timestep larger or smaller according to the force at a certain moment and thus keep the change in speed per timestep more or less constant. We could do this for the whole system of particles, but this could easily result in an unacceptable increase of the total running time. However, it is also possible to assign each particle it's own individual timestep, which is of course much more efficient, although this results in many practical problems, especially with the Tree-Code and Particle-Mesh codes:
If particles come very close to each other, their interaction may show a more complex behaviour than the simple gravitational or Coulomb interaction. For example extra, more progressive repulsive components may occur, as is the case with interacting atomic particles.
It is also possible that they collide using the simple mechanical collision laws for either central elastic or central non-elastic collisions as is the case with particles that interact through the gravitational interaction. Partly non-elastic collisions and non-central collisions are very complicated to deal with and are considered to be beyond the scope of this report.
Finally we could ignore all collisional effects if they don't play a significant role, as we do in Particle-Mesh.
Some of the techniques will be discussed in short hereafter :
As the Particle-Mesh method ignores pairwise interaction (it can only be applied to systems of more or less uniform distributed particles), it is not possible to deal with collisions here.
In fact we should stop the particle-mesh simulation if to many particles come to close to each other : it is supposed to be used only for (almost) collisionless systems.
Unfortunately, checking the relative positions to determine if we have to stop, can only be done if we check the pairwise interparticle distance and that was exactly what we wanted to avoid as it introduced the O(N2) scalability of the Particle-Particle method. But, this can be improved if we only check for particles in the current cell and its neighbours, but even this causes a lot of extra calculations.
This is being done in a more enhanced version of Particle-Mesh, that uses the Particle-Particle approach for particles close to each other : Particle-Particle-Particle-Mesh or P3M, so here it would be possible to add collision management, but also the P3M method is beyond the scope of this report.
Elastic collisions occur if colliding particles do not change their individual particle mass and shape during the collision : only kinetic energy and momentum are being exchanged and nothing else. Note that elastic collisions can only be calculated for central collisions: for non-central forces we need more information about the change in direction for at least one of the particles.
However, this is in general no problem for 2 different reasons :
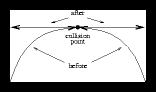
How should we calculate the new speeds after a central elastic collision occurred ?
Although this is plain classical mechanics I'll discuss this briefly hereafter, to save other people the time of either searching for this in other places or to derive this themselves :
From the laws of energy and momentum conservation it follows that at every time the total momentum in all directions and the total energy should be all constant. So, for the momentum and energy before and after the time of impact we may write :
| ||||||||||||||||||||
Here ' v ' denotes the speed before collision, ' w ' the speed after collision.
Also, if we transfer this system to the centre-of-mass system (with speed vc ), the total momentum within this centre-of-mass system must be necessarily zero. This makes the computation quite easy as from energy conservation follows that - although the direction of the momentum may change - the magnitude of the momentum stays the same for all individual particles :
| |||||||||||||||||||||||||
Note that in the centre-of-mass system the collision is always a frontal collision ! The centre-of-mass speed vc used in the equations above is given by :
| (26) | ||||||||||||||||||
And this altogether yields us the equations that enable us to calculate the new speed components after a central elastic collision between two particles :
| (27) | ||||||||||||||||||||||||||||||||
Another possible interaction could be that the two colliding particles become ``clogged'' and continue from now on as if they were one new particle with the total mass, speed and energy of the old ones. There are 2 ways to achieve this without reducing the number of particles (which is sometimes difficult from a software point of view, especially on a distributed memory machine) :
Also note that all non-elastic collisions have another impact on the pairwise potential energy: non-elastic collisions do not conserve energy ! This implies that checking the total energy before and after the simulation can be pretty useless, unless the internal energy stored in the joined particles is also taken into account.
As for the equations for the non-elastic collision: they are even more simple than those for the elastic one.
The new mass for both particles becomes :
| |||||||||||||||
The new speed can be found by assignment of the total momentum to one particle and then divide this by the total mass and give the other one a zero speed :
| (28) | ||||||||||||||||||||||||||||
And the new position is simply that of the centre-of-mass for one and an arbitrary value (0 !) for the other :
| (29) | ||||||||||||||||||||||||||||
Note that the change of mass needs some special arrangements on a distributed memory system : normally only the particle positions need to be updated from the other slaves, but if we allow non-elastic particles we should also update the particles masses at every iteration step !
As said already: it is also possible to add an extra repulsive component to the force. This extra component should only become important at short distances and so it should drop faster with the distance than the [1/(r2)] force. To avoid this component becomes significant at distances of about 1 , it also needs a small constant. The total force then becomes something like :
| (30) |
With c1 quite large (i.e. > 1000 ) and c2 larger than 2 (i.e. 4 ).
The calculation of the extra force component takes some more time if we do it for all particle interactions, but it is perfectly possible to only calculate this for particles that are close to each other, provided the component is small enough. We have to check for this distance anyway, so it virtually doesn't add any extra calculations to our simulation.
Note that this extra component should also be taken into account for the total energy computation (see equation 17) or else problems may arise with energy conservation, although the contribution on larger distances is often neglectable.
In practice it seems that this method is probably the most widely used type of collision management, although I choose the elastic collision to be the default for my simulations.