The Particle-Mesh method is one of the oldest improvements over Particle-Particle, introduced somewhere around 1985 by R.W. Hockney & J.W. Eastwood (see []). In the PP method we only discretize the time-step, but in the PM method also the spatial coordinates are being discretized by setting up a rectangular grid over the particle space (either 2D or 3D).After we choose the appropriate grid (which should be large enough to avoid any particles moving outside the grid during the simulation !), the particle masses are assigned to the nearest grid points. This can be done very simplistic such as is the case with ``Nearest Grid Point'' or in a more advanced way like i.e. ``Cloud In Cell'' (explained later).
After that we could simply use the PP method to calculate the total force on each particle by summing all contributions of all meshpoints, just as if they were normal particles. However, this would only give us an advantage if the number of meshpoints ( M ) is much less than the number of particles ( N ), which could lead to intolerable discretisation errors. It also introduces many practical problems, such as what would happen if a particle is exactly located on a meshpoint (which results in a singularity !). For these reasons this method - although it is the first that comes in mind if you're totally new in these matters :-) - is almost never used.
But there is a much more clever technique that results in a dramatic decrease of the number of computations: As soon as we have assigned the particle masses to the gridpoints, we have in fact created a ``density distribution'' and according to ``Gauss law'' there is a relation between the density r(x,y) and the divergence of the field (which is Ñ·E(x,y) in case of a Coulomb force and Ñ·a(x,y) in case of a gravitational force) :
| (1) |
But, as the gradient of the potential ( ÑF) - which is in itself is a scalar field - at a certain location is by definition always equal to the vector field E ,
| (2) |
| (3) |
The constant c is determined by the nature of the force : it equals -[1/(e)] for the Coulomb force and 4pg for the gravitational force with 3D problems.
An important problem arises with the definition of the density: in 2D simulations as we use here the density is not mass or charge per unit of volume, but mass or charge per unit of area ! This fundamentally changes the nature of the force if the Poisson equation is used (see table ). This has to be kept in mind if we want to be able to compare the simulation output for PP and for PM.
|
E | r | F | F | Example in 3D | |
| 1D | [c·Q/2] | [Q/l] | ~ | r| | C | 2 charged plates |
| 2D | [c·Q/(2pr)] | [Q/A] | ~ log| r| | ~ [1/| r| ] | 2 charged wires |
| 3D | [c·Q/(4pr2)] | [Q/V] | ~ [1/| r| ] | ~ [1/(r2)] | 2 charged particles |
The Poisson equation from above would be an easy one to solve if we'd know the potential and we wanted to find the density. However, life isn't always that easy: in the case of a known density and an unknown potential we have to solve an integral equation instead.
But fortunately a man called Joseph Fourier invented an amazing mathematical trick to solve this problem : ``Fourier Transforms'' or ``spectral analysis''. If the Poisson equation from above is transformed into the so called ``frequency domain'' using a (spatial) Fourier Transformation, the differential equation changes into an algebraic equation that can be easily solved :
|
The Fourier coefficient [75\vec] is just the vector of elements (k,l) , but as it is squared this simply results in its inner product k2+l2 . The term i2 only gives us an extra minus sign and so we find for the transformed potential :
| (4) |
Transforming back to the spatial domain using ``Inverse Fourier Transforms'' gives us then the potential F(x,y) , which can be used to calculate the field E(x,y) in every meshpoint (which is either the electric field or the acceleration).
With this information we can find the ``exact'' field at the particle location by using some interpolation technique and then we can directly calculate the new position and speed of the particle using one of the integration methods as described in section .
How the mass-assignment, the Fourier Transforms (that should be discrete ones because of the spatial discretisation) and the field interpolation are done, is something I'll discuss in more detail hereafter.
Roughly the complete algorithm looks as in table :
|
- calculate the total energy and momentum |
| - initialise the mesh (dimensions, memory) |
| - set the timecounter to 0 |
| - while ( timecounter < endtime ) |
| - for all particles do |
| - compute density r by assigning mass to nearby meshpoint(s) |
| (using either NGP or CIC) |
| - endfor |
| - calculate Fourier Transformed density [(r)\tilde] on the mesh |
| - calculate (FFTed) potential [(F)\tilde] on the mesh using Poisson's |
| equation ( Ñ2F = c.r) |
| - find potential f using an Inverse Fourier Transform |
| - for all particles do |
| - compute the field (acceleration) in nearby meshpoints ( [69\vec] = -Ñf) |
| - interpolate the field at the particle position |
| - calculate new speed and position using a suitable scheme |
| - endfor |
| - write or plot the new particle positions |
| - increase timecounter with the timestep |
| - endwhile |
| - check the energy and momentum for conservation |
A word about the boundary conditions for particle problems: in most simulations there is an infinite particle space, that is simulated by using so-called ``periodic boundary conditions''. The mesh should be sufficiently large to insure that no particle would move outside the particle space during the intended time of the simulation.
However, particles moving in for example a box with solid walls could be simulated as well by applying different boundary conditions: in this case ``Neumann boundary conditions'' have to be set, resulting in the speed being always 0 at the boundaries. For more information about boundary conditions the reader is referred to [] or [].
To find the density in the gridpoints, we need to use a technique to assign the particle masses to the gridpoints. Two of the most well-known methods will be briefly discussed: a zero-order and a first-order one. (See for a discussion of the 1D version [] and [])
To find the density (which is mass per unit of the dimension, i.e. length for 1D, area for 2D and volume for 3D) we have to scale the mass with the size of one cell. It may be a good idea to scale the masses with the size of one cell (2D: cellsize.x * cellsize.y) at initialisation time and thus use a ``scaled'' mass, to avoid having to do this every time the mass assignment is carried out.
Note that the gridpoints are in my implementation chosen to be in the centre of each mesh cell and not on the edges.
This method is very simple and is the same for 1D, 2D or 3D: For each particle just look for the gridpoint that is closest and then assign (add) all the mass of the particle to the mass concentrated in that gridpoint (the cell centre). This is in fact a zero-order interpolation.
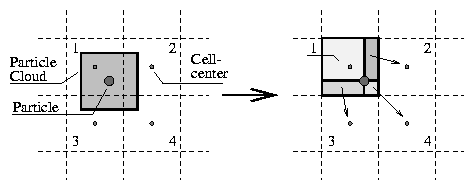
The most popular method is a technique called ``Cloud-In-Cell''. It looks for the 2 nearest gridpoints in a 1D simulation, the 4 nearest ones for a 2D simulation etc. Then it calculates the distances from the particle to these points and assigns each of the 2,4 or 8 nearest gridpoints a weighted part of the total particle mass.

In figure 1 my interpretation of the CIC method for 2D is shown graphically : The particle is surrounded by a ``cloud'' exactly the same size as one individual cell. This cloud overlaps at most 4 cells in the 2D case. The relative size of the overlapping areas for each cell is the scale factor that is used to assign the particle mass to the corresponding cell.
As shown in the right part of the figure, the cell that contains the particle can be used to calculate all necessary information for the other 3 cells as well. This approach saves some calculation time if compared with the left part but otherwise yields exactly the same results.
After assignment of the particle masses to the mesh, it is time to convert this density distribution into a potential distribution on the mesh. In the introduction the general method, based on Fourier transforms was already discussed. However, we do not have a density function, but only a density distribution. As a result, we will only be able to find a potential distribution, not a potential function. So, instead of differentiating (taking the gradient) we can only use finite differences between the gridpoints.
Equation 3 can be written in the form of a finite difference equation ( in this case it is a ``2nd order centred finite difference equation'' ) :
| (5) |
or for the 2D case :
| (6) |
As with the continuous case above, this is a so called implicit problem, that could not be solved in a straightforward manner. One popular technique is Gauss elimination, applied on a tridiagonal (1D) or pentadiagonal (2D) matrix. Another one, which is the one I choose to use here, is through a Discrete Fourier Transform, which is in many ways analog to the discussion for the continuous part in the introduction :
| (7) |
and again for the 2D situation :
| (8) |
Using a little math (Euler's formula) we can rewrite this into :
| (9) |
And this results (using the relation cosx-1 = -2sin2([1/2]x) ) in :
| (10) |
|
Substitution then yields an equation that closely resembles the continuous Fourier transformed Poisson equation 4 we saw before in the introduction :
| (11) |
As could be easily seen K and L could just be replaced with k and l if the mesh spacing would be infinitely small: since quite some time (:-)) the limDx® 0[(sin(Dx))/(Dx)] = 1 . But unfortunately the essence of finite difference is that the spacing is not infinitely small .....
Ok, above we have discussed in detail how to obtain the Fourier Transformed potential from the Fourier Transformed density distribution. Now it is time to take a closer look at the Fourier Transform routine for a discrete set of numbers itself. It is crucial that this transformation goes fast enough or else we could as well use the PP method instead and forget about all the nasty stuff above.
First we'll take a look at the standard routine, the Discrete Fourier Transform (DFT), just to be able to understand how it works. Unfortunately for the DFT the number of computations to transform a set of N numbers scales with N2 and as such it isn't of much practical use. But, I needed a simple algorithm that worked flawlessly, to be able to check the results of the other, superior routine I want to discuss: the Fast Fourier Transform (FFT).
Of course there are many versions for the DFT and FFT available on the net (i.e. NETLIB or NAG) , but most of them are in Fortran and if there is one thing I want to avoid as long as possible it is Fortran (:-). Also there were much less implementations for 2D Fourier Transforms, even in Fortran , and the C versions I saw were so clumsily written (mostly directly transferred from Fortran to C) that I decided to setup my own C library (and distribute it on the net for other people who are interested).
The exact so called ``Discrete-time (!) Fourier Transform'' (do not confuse this with the DFT !!) and it's inverse look as follows:
| ||||||||||||||||||||||||||
Of course the summation from -¥ to ¥ is impossible to carry out on a computer, where we only have a limited number of samples. We also only want to store a limited number of frequencies in the Fourier domain, which makes the integral also problematic.
For this reason the ``Discrete Fourier Transform'' was invented, which is devised in such a way that we have exactly as many frequencies in the frequency domain as we have samples in the spatial (or time) domain. This turns both formules into a summation over a limited number of either N samples or N frequencies. Also in this case we do not store the frequency itself, but the wavenumber k , where the frequency is given by Wk = k·[(2p)/N] . This results in the following set of equations for the DFT :
| (12) | ||||||||||||||||||||||||
When using a computer it is often easier to rewrite the complex terms into their separate real and imaginary parts (except if you use Fortran, but as said before : that's out of the question in my case, although I must admit the complex type in Fortran isn't a bad thing at all :-).
If we do so, the first equation (the ``analysis'' in 12) expands to :
| (13) | ||||||||||||||||||||||||||||||||||
And the second equation (the 'synthesis' in 12) will look like :
| (14) | ||||||||||||||||||||||||||||||||||
As you can see these two routines are almost identical apart from 2 ' - ' signs and a scale factor. For this reason often only one routine is used for both transformations. In that case a small flag is used to put the right signs at the right place.
A few remarks:
| |||||||||||||||||||||||
Where the righthand side is the right band and the lefthand side is the left band of the Fourier transform.
The Fast Fourier Transform, discovered somewhere about 1965, is an algorithm that computes exactly the same result as the DFT described in the previous part, it only does this tremendously faster, especially for high N , as the number of computations for the DFT scales with O(N2) , while the FFT scales with O(N·logN) .
I am not going to discuss the FFT here, but only mention a few things to bear in mind when using the rather simple library I build for it.
A fine (and highly readable !) description of the FFT is given in [], although the provided code is somewhat clumsy as it was directly derived from Fortran. Nevertheless, my own code was loosely based on these examples as they are very simple and straightforward.
A few remarks :
Everything discussed so far only concerns the 1D Fourier Transform. However, we have to transform over 2 dimensions in our case. This is done by first transforming all the rows separately and after that all the columns. So, for a N·M mesh we have to do N transforms of vectors with length M and M transforms of vectors with length N . This results in a total number of FFT's (and also inverse FFT's) of N+M (for each timestep !).
A practical problem is the memory layout in a computer: this is still only one dimensional, so all rows and columns of the mesh lay behind each other. This implies that we can either pass the address of a row to the FFT - assumed that all the row elements are in one contiguous memory area -or the address of a column - in case all column elements are in one contiguous area - but certainly not both.
So if we want to use the same FFT routine for both the rows and the columns, we have to swap all elements in the rows and columns halfway the transformation !
As said in the previous section, both N and M should be a power of 2, although it is not necessary to give them both the same value, although this causes extra problems in transposing the matrix halfway (see algorithm) and it requires 2 different cosine lookup tables. Note that the order is unimportant, as long as we do not execute both at the same time ....
The 2D algorithm roughly looks as in table .
- if it's the first call: generate a sine/cosine lookup table for
the given dimension to speed up calculations
- else if given dimension is different from lookuptable size:
generate an error
- set all elements in target matrix to zero
- for (row=0; row<dim; row++)
- fft1d(source[row],target[row],dim,signflag)
- endfor
- transpose the target matrix, now filled with transformed rows
- for(col=0; col<dim; col++)
- fft1d(target[col],source[col],dim,signflag)
- endfor
- ready
After that we've found the potential on the mesh, we actually have had the worst part (sigh). Now comes the calculation of the gravity field (which is simply the acceleration !) or the electrical field on the mesh and thereafter the interpolation of the field for all particle locations. Using formula 2 we can relatively easy find the field if we know the potential. The known and unknown part are interchanged if compared with the Poisson equation, which leads to a simple, straightforward problem.
But - as always - there are a few quirks to be counted with. In the discretised version we (or at any rate I) would tend to write equation 2 as follows :
|
But consider what would happen if a particle is located at exactly meshpoint x ? In that case we would find a field in meshpoint x that virtually only contains the contribution of that particular particle. So the field at the particle location (which is also x ) will be exacly that same field !
In other words : the particle only ``feels'' it's own influence, and a so-called ``selfacting force'' works on the particle, which of course leads to nonsense results. (Consider for example the earth: it will never start moving only because of it's own gravity field !!) But, selfacting forces can be easily avoided by applying ``central differencing'' instead :
| (15) |
In that case the contribution of the particle in meshpoint x will be exactly cancelled out, as its influence on Fx+1 is precisely the same as on Fx-1 .
Now that we know the field in the meshpoints, we can interpolate between the meshpoints to find the field at the particle location. This is in fact a similar (but reversed) problem as the mass-assignment to the mesh. For reasons I won't discuss here in detail, it is important to use exactly the same interpolation method as in the mass-assignment, to avoid loss of momentum and the introduction of large numerical errors. Main problem is the introduction of ``selfacting forces'' in the simulation if this rule is neglected.
So, if we did the mass-assignment using NGP, we should also use an (inverse) NGP for the field interpolation and if we used CIC we should use an inverted CIC to find the field. This ensures, together with the central differencing from above, that the force of particle A on B will be exactly the opposite of the force of B on A.
For further information the nice article by Peter MacNeice ([]) and of course the ``Holy Bible'' for Particle Mesh methods by Eastwood and Hockney ([]) are strongly recommended.
While building the program a lot of little and bigger practical problems had to be solved. I just want to mention a few points hereafter :
As with PP, there are many variables that can be used to alter the specific behaviour of the simulation. In the datafile the stepsize, the number of iterations and the number of iterations between a screen update can be specified. For the exact meaning of the datafile layout, see the appropriate appendix in .
Commandline options :
00.00.0000
The same graphical interface as used for PP is also used for the PM program, so the remarks in the PP chapter also apply here. There is however one thing I'd like to add here:
To check the density and potential distribution I used a circle with a radius proportional to the meshvalue, to give some graphical indication about these distributions. This of course made development significantly easier. Because of the large differences between small and large values I decided upon a logarithmic relation between radius and meshvalue. But, unfortunately some graphic libraries (at any rate the one that was developed by me ) , only use the magnitude of the supplied radius to draw a circle !
That is no problem in most cases, but in the case of a logarithm this could be disastrous: an ascending series like 10-2, 10-1, 1, 10, 102 would be represented on the screen by circles with radius 2, 1, 0, 1, 2 : a symmetric one, so 10-2 would be equal to 102 !
I did spend 2 full days debugging to find out why my DFT and FFT wouldn't work until finally I found they worked perfectly well : only the visualisation failed because of the problem above. If this warning could save only ONE person from making the same mistake it is already worth the trouble mentioning it here, isn't it ?
From all 3 methods described in this report, the Particle-Mesh method is the fastest, provided we're talking about a large number of particles. However it has some restrictions that are possibly already clear to the reader, but I like to mention them hereafter for completeness :