Chapter 7
Results and conclusions

1.  Results

First let's take a look at some non-uniform sets (only runtime and energy are shown, the error in the momentum is omitted to avoid giving too much rather meaningless information). Also the results for the 3 non-uniform sets from the previous section can be found in here (see table ).

The run for 4 particles couldn't be completed with PM as one particle moved outside the mesh. The error in the energy is now for only 2624 iterations, so about one third of the other 2.

Note that PM always uses a meshsize of at least 32x32, which results in runtimes of about the same order for all problems except for 2000 particles, where the meshsize was increased to 64x64.

There is another important remark to be made : in all cases we can say that - as long as the number of iterations and the timestep are identical - PP must necessarily have the largest accuracy. If there are large errors in the PP results they are almost always caused by collisions and close encounters.

Well, TC is as vulnerable for close encounters as PP and so should have more or less the same error as PP, as long as the error made by the tree approximation is small compared with this error. So, the closer the error to the error made in PP, the more likely it is that the TC approximation is indeed a good one !

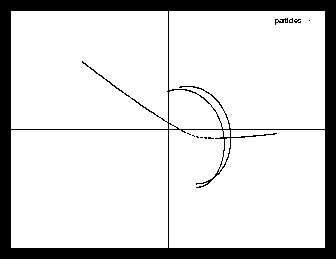
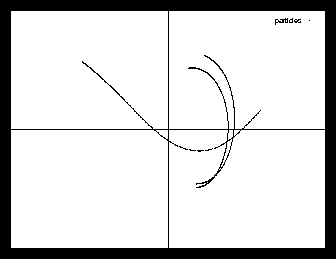
PM does not suffer from collisions and so also doesn't have the problem with energy leaks in close encounters. Energy (and also momentum) are often reasonably well preserved. However, all details caused by the close encounters are completely washed out or blurred too. I.e. the 4 body example from the introduction (with the sun, the planet and the moon: see picture ) runs fine with both TC and PP, but shows something that only vaguely resembles these pictures if run with PM (see picture 1).

Now let's take some uniform sets and do the same comparison. Table shows the results for the smaller meshes (where PP was still practically possible).

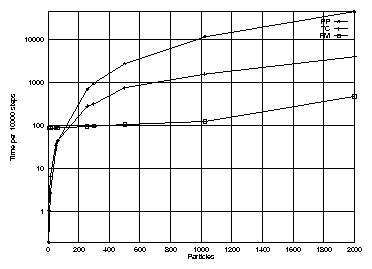
If we put all results from the tables 1 and 2 in a picture we could compare the efficiency for PP, PM and TC. We see in figure that indeed the computation time for PP increases much faster than for PM and TC. It is also nice to see that TC computation time increases smoothly with the number of particles, while PM stays constant for a while, but suddenly jumps if the meshsize has to be increased. The latter stems from the fact that the FFT routines only accept meshsizes that are a power of 2.

I also ran some larger uniform problems - both meshes and random sets - on only PM and TC, to see what their relative accuracy is and what the scaling of the computation time looks like. These larger problems - all generated by the 2 helper programs as mentioned earlier - are the same ones as already discussed in the Auto-Correlation section of chapter .

A special problem arose with the computation of the energy error : the potential energy computation is unfortunately an order O(N²) operation. This implies that for the large problems the bulk of the time would be spent in the energy error computation and not in the simulation part ! To give an idea : the total runtime for 131072 particles while doing the energy error computation was about 10 hours for PM and about 10.5 hours for TC, so this computation of the potential energy made the difference between PM and TC almost completely being washed out if only the total running time is being used.

For real large problems it may be an idea to use a Poisson equation and an FFT to compute an approximation of the potential energy, just as was done in the previous chapter (Analysis).

The output for Tree-Code and the generated sets can be found in table 3, while the same results for Particle-Mesh can be found in . For reasons explained before the runtimes given in these tables are the runtimes without the initialisation and energy error computation.

To give an idea about the complexity of these problems, the number of computations for O(N²) and O(N·logN) operations for all the used combinations of particles and iteration steps is given in table .

As should be clear when comparing the numbers from table 5 with the results from the tables 3 and 4, the runtimes increase a little faster than should be expected if we consider that both methods are supposed to scale with O(NlogN) . There are however several explanations for this phenomenon :

• Most modern computers have one or more levels of fast cache memory between the processor and the relatively slow main memory. This implies that the performance can drop dramatically as soon as the size of the problem becomes larger than the cache size on one or more levels.
  I checked this sometime ago and found that increasing a problemsize with only 10 %, in worst case situations sometimes results in a runtime that could be more than 10 (!!) times as long as before, only because of these cache effects. As the difference in our case is on average only about a factor 2 to 3, it is reasonable to assume this was indeed caused by caching.

• The number of computations for PM does not directly depend on the number of particles, but on the number of gridcells. Going from 256x256 to 512x512 (as with the step from 65536 to 131072 particles) does not double the number of computations, but of course increases them with a factor 4. So the runtime is in this case almost exactly what we expect for a O(NlogN) behaviour if we take N as the number of cells instead of the number of particles.

• The recursion with Tree-Code makes heavily use of the stack, sometimes leading to a lot of extra time spent in pushing and pulling return addresses to and from the stack.
  Furthermore the coordinates are currently only sorted on their X-coordinates and not on both, so in reality the order for the Tree-Code is currently something like O(N[ÖN)] , provided of course that a reasonable uniformity exists.
  On the other hand: the weighting factor for the particle count is only small as the time needed for one operation (a particle count in the sortlist) is short compared with the much heavier other operations like the acceleration computation.

2.  Conclusions

In the introduction I have listed some of the targets for this research project. I think I can say that most of the targets have been reached. However, although I did work already 2 years ago on the parallelization of the PP method described in this report, and although I have already done some work for the parallelization of the TC and PM programs as well, I didn't find the time to complete this unless I would be satisfied with only doing half work, resulting in i.e. a very poor speedup.

For this reason and also because this report is already quite a bit longer than I intended it to be at the beginning, I decided to omit the parallelization part completely and put the results in a separate report, to be submitted probably next year.

Ok, now it is the time to summarize some of the conclusions resulting from this report :

• For large problems Particle-Mesh is certainly the fastest method, but it blurs many of the details. It behaves very bad for relatively small and for non-uniform problems as well as for problems where many collisions are likely to happen. This is why it should be only recommended for more or less uniform, collisionless systems.

• The Tree-Code method described in this report is quite accurate, provided the discriminating factor Q is large enough and it is also reasonably fast even for these larger values of Q. Another advantage is that it allows for the proposed collision management methods described earlier in this report.

• The ``sort and count'' technique to build a tree for the Tree-Code problems as described in this report - although discovered more or less accidently through a misunderstanding made by me - proves to be indeed a practically useful method, provided optimal sorting techniques are being used. However, it still needs to be compared with a Tree-Code algorithm according to the standard Barnes-Hut method to see if it really can be faster.

• Within uniform distributions, forces that act only over a short distance in a 2 dimensional simulation may turn into long-distance forces if the same problem is transferred to 3 dimensions. This has to be kept in mind if - as was done in this report - only 2 dimensional problems for gravity and electric forces are being studied just because they are easier to visualize.

• As shown in chapter a rough distinction between sets suited for TC, PM or PP can indeed be made by looking at the auto-correlation for the density distribution, together with the ratio between the average displacement over the intended simulation interval and the average minimum interparticle distance.

• At the risk of reopening an already open door : The ``leapfrog'' integration method is the most simple integration method that guarantees a reasonable accuracy. `\"Runge-Kutta'', although quite accurate for only a few integration steps, is not recommended for simulations over a longer period due to it's numerical instability.

• O(N·logN) behavior - although theoretically available in both TC and PM - is practically difficult to realize, except for relatively small problems. As soon as memory cache sizes are exceeded, on most of the modern computer architectures the runtime tends to grow slightly faster with increasing N than the theory suggests.