References

1

C.C. Ashcraft and R.G. Grimes. On vectorizing incomplete factorization and SSOR preconditioners. SIAM J. Sci. Stat. Comput., 9:122-151, 1988.

2

W.L. Chen, F.S. Lien, and M.A. Leschziner. Computational modelling of turbulent flow in turbomachine passage with low-Re two-equation models. In S. Wagner, E.H. Hirschel, J. Périaux, and R. Piva, editors, Computational Fluid Dynamics '94, pages 517-524, John Wiley and Sons, Chicester, 1994.

3

Y.-S. Chen and S.-W. Kim. Computations of turbulent flows using an extended k- turbulence closure model. Report NASA CR-179204, NASA-Marshall Space Flight Center, Alabama, USA, 1987.

4

I.A. Demirdzic. A finite volume method for computation of fluid flow in complex geometries. PhD thesis, University of London, 1982.

5

S.C. Eisenstat. Efficient implementation of a class of preconditioned conjugate gradient methods. SIAM J. Sci. Stat. Comput., 2:1-4, 1981.

6

P.H. Gaskell and K.C. Lau. Curvature-compensated convective transport: SMART, a new boundedness-preserving transport algorithm. Int. J. Numer. Methods in Fluids, 8:617-641, 1988.

7

T.B. Gatski and C.G. Speziale. On explicit algebraic stress models for complex turbulent flows. J. Fluid Mech., 254:59-78, 1993.

8

V. Haroutunian. Simulation of vortex shedding past a square prism using three two-equation turbulence models. In Sixth Int. Symp. on CFD, volume 1, pages 408-414, Lake Tahoe, Nevada, 1995. A collection of technical papers.

9

C. Hirsch. Numerical Computation of Internal and External Flows. Vol.1: Fundamentals of Numerical Discretization. John Wiley, Chichester, 1988.

10

M. Kato and B.E. Launder. The modelling of turbulent flow around stationary and vibrating square cylinders. In Proc. Ninth Symposium on Turbulent Shear Flows, volume 9, page 10.4.1, Kyoto, Japan, 1993.

11

C.D. Kay. Schaum's outline of theory and problems of tensor calculus. McGraw-Hill, New York, 1988.

12

P. K. Khosla and S. G. Rubin. A diagonally dominant second-order accurate implicit scheme. Comput. Fluids, 2:207-209, 1974.

13

B. Koren. A robust upwind discretization method for advection, diffusion and source terms. In C.B. Vreugdenhil and B. Koren, editors, Numerical methods for advection-diffusion problems, pages 117-137, Vieweg. Braunschweig, Wiesbaden, 1993. Notes on Numerical Fluid Mechanics 45.

14

C.K.G. Lam and K. Bremhorst. A modified form of the k- model for predicting wall turbulence. ASME J. Fluids Engng., 103:456-460, 1981.

15

B.E. Launder and D.B. Spalding. The numerical computation of turbulent flows. Comp. Methods Appl. Mech. Eng., 3:269-289, 1974.

16

F.S. Lien and M.A. Leschziner. Upstream monotonic interpolation for scalar transport with application to complex turbulent flows. Int. J. Num. Meth. Fluids, 19:527-548, 1994.

17

J.A. Meijerink and H.A. Van der Vorst. An iterative solution method for linear systems of which the coefficient matrix is a symmetric M-matrix. Math. Comp., 31:148-162, 1977.

18

H.K. Myong and N. Kasagi. unknown. J. Fluids Engng., 112:521, 1990.

19

S. Nisizima and A. Yoshizawa. Turbulent channel and Couette flows using an anisotropic k- model. AIAA J., 25:414-420, 1987.

20

C.C. Paige and M.A. Saunders. LSQR: an algorithm for sparse linear equations and sparse least square problem. ACM Trans. Math. Softw., 8:44-71, 1982.

21

R. Rubenstein and J.M. Barton. Non-linear Reynolds stress models and the renormalisation group. Phys. Fluids A, 2:1472, 1990.

22

Y. Saad and M.H. Schultz. GMRES: a generalized minimal residual algorithm for solving non-symmetric linear systems. SIAM J. Sci. Stat. Comp., 7:856-869, 1986.

23

H. Schlichting. Boundary layer theory. McGraw Hill, New York, 1969.

24

A. Segal. The treatment of slip boundary conditions for the incompressible navier-stokes equations in general co-ordinates. Report 91-22, Faculty of Mathematics and Informatics, Delft University of Technology, Delft, 1991.

25

A. Segal and K. Kassels. Some 2d test examples for the isnas incompressible code. Report 91-44, Faculty of Mathematics and Informatics, Delft University of Technology, Delft, 1991.

26

Guus Segal and Kees Kassels. Improvements of the discretization of the incompressible Navier-Stokes equations in general coordinates. Report 96-81, Faculty of Technical Mathematics and Informatics, Delft University of Technology, Delft, 1996.

27

P. Sonneveld. CGS, a fast Lanczos-type solver for nonsymmetric linear systems. SIAM J. Sci. Stat. Comput., 10:36-52, 1989.

28

D.B. Spalding. A novel finite difference formulation for differential expressions involving both first and second derivatives. Int. J. Numer. Methods in Engineering, 4:551-559, 1972.

29

C.G. Speziale. On nonlinear k-l and k- models of turbulence. J. Fluid Mech., 178:459-475, 1987.

30

P.K. Sweby. High resolution schemes using flux-limiters for hyperbolic conservation laws. SIAM J. Num. Anal., 21:995-1011, 1984.

31

H. Tennekes and J.L. Lumley. A First Course in Turbulence. MIT Press, Cambridge, Massachussets, 1982.

32

H.A. Van der Vorst. Iterative solution method for certain sparse linear systems with a non-symmetric matrix arising from PDE-problems. J. Comput. Phys., 44:1-19, 1981.

33

H.A. van der Vorst and C. Vuik. GMRESR: a family of nested GMRES methods. Num. Lin. Alg. Appl., 1:369-386, 1994.

34

J.J.I.M. Van Kan, C.W. Oosterlee, A. Segal, and P. Wesseling. Discretization of the incompressible Navier-Stokes equations in general coordinates using contravariant velocity components. Report 91-09, Faculty of Technical Mathematics and Informatics, Delft University of Technology, Delft, 1991.

35

B. van Leer. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method. J. Comput. Phys., 32:101-136, 1979.

36

C. Vuik. Termination criteria for GMRES-like methods to solve the discretizet incompressible navier-stokes equations. Report 92-50, Faculty of Technical Mathematics and Informatics, Delft University of Technology, Delft, 1992.

37

C. Vuik. Solution of the discretized incompressible Navier-Stokes equations with the GMRES method. Int. J. Num. Meth. Fluids, 16:507-523, 1993.

38

D.C. Wilcox. Reassessment of the scale determining equation for advanced turbulence models. AIAA J., 26:1299-1310, 1988.

39

D.C. Wilcox. A half century historical review of the k- 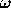model. AIAA Paper 91-0615, 1991.

40

V. Yakhot, S.A. Orszag, S. Thangam, T.B. Gatski, and C.G. Speziale. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A, 4:1510-1520, 1992.

41

M. Zijlema. On the construction of a third-order accurate TVD scheme with application to turbulent flows in general domains. Int. J. Numer. Meth. Fluids, 1995. To appear.

42

M. Zijlema. Computational modeling of turbulent flows in general domains. PhD thesis, Delft University of Technology, The Netherlands, April 1996.