IF IT WALKS LIKE ....
by Jos van Kan.
Playing Imps you hold as west in 4th seat, all vulnerable  96
96  K9765
K9765  8765
8765 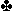 K3 and partner opens in
second seat with 1
K3 and partner opens in
second seat with 1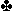 . RHO overcalls 1
. RHO overcalls 1 and you have just enough for a negative double. This earns little respect
from LHO, who jumps to 3
and you have just enough for a negative double. This earns little respect
from LHO, who jumps to 3 , partner passes
and RHO goes to game. So the bidding has been:
, partner passes
and RHO goes to game. So the bidding has been:
| west |
north |
east |
south |
| -- |
pass |
1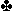 |
1 |
| X |
3 |
pass |
4 |
| pass |
pass |
pass |
|
You lead 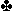 K and the dummy comes
down with
K and the dummy comes
down with
Partner encourages with 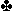 8, you
continue Clubs and partner wins with
8, you
continue Clubs and partner wins with 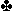 Q
as declarer follows to both rounds (with 4 and 6). Partner now surprisingly
switches to
Q
as declarer follows to both rounds (with 4 and 6). Partner now surprisingly
switches to  T, won in dummy with
the
T, won in dummy with
the  Q and declarer continues with
a second round of trumps on which partner tosses a
Q and declarer continues with
a second round of trumps on which partner tosses a  ,
as declarer wins the Ace. Declarer continues with
,
as declarer wins the Ace. Declarer continues with  Q
from hand.
Q
from hand.
-
Who has
 A? Who has
A? Who has  Q?
Q?
-
How many Clubs does partner have at least?
-
Who has
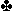 9?
9?
-
How many tricks does declarer have? <br> a) if partner has 6 clubs <br>
b) if partner has 5 clubs
-
How do you defend?
-
At this point there are 3 picture cards whose location is unknown:
 A,
A,  Q
and
Q
and  J. Partner, who has opened
the bidding only has shown up with AQ of clubs and hence certainly has
J. Partner, who has opened
the bidding only has shown up with AQ of clubs and hence certainly has  A.
He probably also has
A.
He probably also has  Q unless
he has extraordinary distribution. He did not bid over 3
Q unless
he has extraordinary distribution. He did not bid over 3 ,
so that is not very likely. He may or may not have
,
so that is not very likely. He may or may not have  J.
J.
-
This is a tricky one. Maybe you'd be inclined to say at least three, but
then you have missed an important inference. He had a singleton
 ,
remember? And a player who has a singleton
,
remember? And a player who has a singleton  (or
(or  ) and opens 1
) and opens 1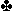 has five or more
has five or more 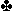 s. Huh?? Yes.
He either has some 5 card or more or exactly 1-4-4-4 distribution.
But that distribution is usually opened 1
s. Huh?? Yes.
He either has some 5 card or more or exactly 1-4-4-4 distribution.
But that distribution is usually opened 1 .
(unless the
.
(unless the  quality is abysmal,
but we have already established that he holds
quality is abysmal,
but we have already established that he holds  Q).
Q).
-
Only of academic value, but nevertheless: declarer has
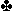 9.
Partner encouraged with
9.
Partner encouraged with 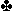 8 and
if he'd had the 9 he'd have played it.
8 and
if he'd had the 9 he'd have played it.
-
If partner has six Clubs declarer has three and he can come to 8 tricks:
5
 , a
, a 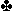 ruff and
ruff and  AK. If partner has five
Clubs declarer has four and he can come to nine tricks since he can now
ruff two clubs.
AK. If partner has five
Clubs declarer has four and he can come to nine tricks since he can now
ruff two clubs.
-
So what kind of problem is this anyway? Isn't declarer bound to go down,
since we are always going to make two
 tricks? Always? Think about it. Suppose declarer has a singleton
tricks? Always? Think about it. Suppose declarer has a singleton  ?
If declarer's
?
If declarer's  Q is singleton you
must be very careful, since otherwise you give it away. Suppose you win
with the K. Now you cannot prevent declarer from ruffing away partners
Ace. So, you must duck the
Q is singleton you
must be very careful, since otherwise you give it away. Suppose you win
with the K. Now you cannot prevent declarer from ruffing away partners
Ace. So, you must duck the  Q
and let partner win his A. He'll play back a
Q
and let partner win his A. He'll play back a  and in the fullness of time you will make either your
and in the fullness of time you will make either your  K
or partners
K
or partners  Q will score.
Q will score.
Post mortem
All this was necessary since the full hand was:
Partner could have made the defense somewhat easier by first cashing  A
before switching to trump. But that would have made it a kind of dull hand.
:-) This is an OKBridge hand and it was played just as I described it.
W was the well known Canadian player Shelagh Paulsson. At the critical
point she ducked the
A
before switching to trump. But that would have made it a kind of dull hand.
:-) This is an OKBridge hand and it was played just as I described it.
W was the well known Canadian player Shelagh Paulsson. At the critical
point she ducked the  K without
so much as pausing for thought! Well done. A question you might still ask
is: "How will declarer know that he must ruff out
K without
so much as pausing for thought! Well done. A question you might still ask
is: "How will declarer know that he must ruff out  A
and not take the
A
and not take the  finesse?" The
answer to that is that declarers ALSO count. Your partner has opened the
bidding and YOU have shown up with two kings already. So your partner must
hold the rest of the HCP and the
finesse?" The
answer to that is that declarers ALSO count. Your partner has opened the
bidding and YOU have shown up with two kings already. So your partner must
hold the rest of the HCP and the  finesse is out of the question.
finesse is out of the question.
copyright © 1997 by Jos van Kan. All rights reserved.
![]() 96
96 ![]() K9765
K9765 ![]() 8765
8765 ![]() K3 and partner opens in
second seat with 1
K3 and partner opens in
second seat with 1![]() . RHO overcalls 1
. RHO overcalls 1![]() and you have just enough for a negative double. This earns little respect
from LHO, who jumps to 3
and you have just enough for a negative double. This earns little respect
from LHO, who jumps to 3![]() , partner passes
and RHO goes to game. So the bidding has been:
, partner passes
and RHO goes to game. So the bidding has been:

![]() A
before switching to trump. But that would have made it a kind of dull hand.
:-) This is an OKBridge hand and it was played just as I described it.
W was the well known Canadian player Shelagh Paulsson. At the critical
point she ducked the
A
before switching to trump. But that would have made it a kind of dull hand.
:-) This is an OKBridge hand and it was played just as I described it.
W was the well known Canadian player Shelagh Paulsson. At the critical
point she ducked the ![]() K without
so much as pausing for thought! Well done. A question you might still ask
is: "How will declarer know that he must ruff out
K without
so much as pausing for thought! Well done. A question you might still ask
is: "How will declarer know that he must ruff out ![]() A
and not take the
A
and not take the ![]() finesse?" The
answer to that is that declarers ALSO count. Your partner has opened the
bidding and YOU have shown up with two kings already. So your partner must
hold the rest of the HCP and the
finesse?" The
answer to that is that declarers ALSO count. Your partner has opened the
bidding and YOU have shown up with two kings already. So your partner must
hold the rest of the HCP and the ![]() finesse is out of the question.
finesse is out of the question.