


Next: Equations governing incompressible
Up: Finite volume computation of
Previous: Finite volume computation of
Solving incompressible turbulent flows using a boundary-fitted coordinate system
is an important technique in CFD. It permits an easy and accurate implementation
of boundary conditions and makes the computation of flows in complex geometries
possible. For this purpose two different approaches can be adopted. The first
approach is a complete transformation of the Navier-Stokes equations to general
coordinates. Such a coordinate-invariant formulation contains many geometric
quantities and thus leads to more work and storage. Moreover, the equations
involve Christoffel symbols which may lead to inaccuracies on non-smooth grids.
Another approach is a partial transformation, in which only the independent
variables are transformed while retaining the velocity components as Cartesian
components. As a result, the governing equations have a strong conservation form
which has a much simpler structure and thus simplifies programming of codes.
The choice of the two approaches mentioned above depends on a grid arrangement:
staggered versus colocated. On staggered grids one may choose Cartesian velocity
components as unknowns in the Navier-Stokes equations, because of simplicity.
But these velocity components, in general, are not perpendicular to grid lines.
Therefore, this approach may lead to unstable discretization. Hence, the
choice of grid-oriented velocity components as dependent variables is preferable.
On colocated grids Cartesian velocity components as primitive variables in the
momentum equations are satisfactory.
In order to compute turbulent flows a turbulence model has to be chosen. Many
investigators adopt isotropic eddy-viscosity formulations, of which a k- model is the most prominent. This model consists of two transport equations for
the turbulent kinetic energy k and its dissipation rate
model is the most prominent. This model consists of two transport equations for
the turbulent kinetic energy k and its dissipation rate  . Both equations
contain a quantity
. Both equations
contain a quantity 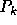 called the production rate of turbulent energy. In the
coordinate-invariant approach this quantity contains Christoffel symbols (in 2D
eight different Christoffel symbols occur). Hence, it seems attractive to
implement the k-
called the production rate of turbulent energy. In the
coordinate-invariant approach this quantity contains Christoffel symbols (in 2D
eight different Christoffel symbols occur). Hence, it seems attractive to
implement the k- model with the Cartesian approach.
model with the Cartesian approach.
In the light of the above observations, the colocated/Cartesian approach for
solving the Reynolds-averaged Navier-Stokes equations with the k- model
has become very popular and has been widely used over the last 15 years
[Habib and Whitelaw, 1982], [Rhie and Chow, 1983], [Peric, 1985],
[Chen and Patel, 1989], [Deng, 1989], [Piquet and Queutey, 1990],
[Lien and Leschziner, 1991], [Cho and Fletcher, 1991], [Melaaen, 1991],
[Coelho and Pereira, 1992], [Zhu and Rodi, 1992], [Xu et al., 1993],
[Rolfes et al., 1993] and [Issa and Oliveira, 1994].
model
has become very popular and has been widely used over the last 15 years
[Habib and Whitelaw, 1982], [Rhie and Chow, 1983], [Peric, 1985],
[Chen and Patel, 1989], [Deng, 1989], [Piquet and Queutey, 1990],
[Lien and Leschziner, 1991], [Cho and Fletcher, 1991], [Melaaen, 1991],
[Coelho and Pereira, 1992], [Zhu and Rodi, 1992], [Xu et al., 1993],
[Rolfes et al., 1993] and [Issa and Oliveira, 1994].
Within the colocated approach the pseudo-compressibility method can also be used.
This has been done e.g. in [Kwak et al., 1986] and
[V. Michelassi and F.
Martelli, 1990]. The former used an algebraic eddy-viscosity
model while the latter used the k- model. The main disadvantage
of this method is that for time-dependent flow problems it is difficult to
obtain accurate mass conservation.
model. The main disadvantage
of this method is that for time-dependent flow problems it is difficult to
obtain accurate mass conservation.
Although the colocated approach is very popular, an important disadvantage of this
approach is that there are special measures required to obtain a stable
discretization (for example the Rhie and Chow interpolation to avoid decoupling
between pressure and velocity).
Staggered grid arrangement has important advantages for incompressible flow
computations, because this arrangement avoids non-physical pressure oscillations.
Some publications discretizing the Reynolds-averaged Navier-Stokes equations for
staggered grids with Cartesian velocity components as primitive variables
including the k- model in general coordinates are [Rapley, 1985],
[Braaten and Shyy, 1986], [Yung et al., 1989] and [Chen et al., 1990]. It
should be recognized that this approach may give rise to unstable discretizations.
Following Chen et al. (1990), the more common way to avoid this, is to
choose the coordinate system such that the angle between the velocity components
and the grid lines is not too large. However, for special domains it is very
difficult to achieve this, especially in 3D.
model in general coordinates are [Rapley, 1985],
[Braaten and Shyy, 1986], [Yung et al., 1989] and [Chen et al., 1990]. It
should be recognized that this approach may give rise to unstable discretizations.
Following Chen et al. (1990), the more common way to avoid this, is to
choose the coordinate system such that the angle between the velocity components
and the grid lines is not too large. However, for special domains it is very
difficult to achieve this, especially in 3D.
Discretizations for staggered grids with grid-oriented velocity components as
unknowns with the k- model are presented in [Pope, 1978], [Rastogi, 1984],
[Demirdzic et al., 1987], [Stern et al., 1988], [Majumdar and Rodi, 1989]
and [Koshizuka and Oka, 1991]. Stern et al. (1988) have formulated the
governing equations in vector notation which has the advantage that Christoffel
symbols do not occur explicitly. Rastogi (1984) and Majumdar et al. (1989)
use contravariant velocity components to solve the Navier-Stokes equations, while
Pope (1978), Demirdzic et al. (1987) and Koshizuka et al. (1991) employ
contravariant physical velocity components as unknowns.
model are presented in [Pope, 1978], [Rastogi, 1984],
[Demirdzic et al., 1987], [Stern et al., 1988], [Majumdar and Rodi, 1989]
and [Koshizuka and Oka, 1991]. Stern et al. (1988) have formulated the
governing equations in vector notation which has the advantage that Christoffel
symbols do not occur explicitly. Rastogi (1984) and Majumdar et al. (1989)
use contravariant velocity components to solve the Navier-Stokes equations, while
Pope (1978), Demirdzic et al. (1987) and Koshizuka et al. (1991) employ
contravariant physical velocity components as unknowns.
In [Mynett et al., 1991], [Wesseling et al., 1992] and
[Segal et al., 1992] a coordinate-invariant discretization of the
incompressible Navier-Stokes equations on a general staggered grid has been
developed. Standard tensor notation has been used. As a consequence, the
formulation contains Christoffel symbols. In spite of that, discretization
accuracy can be maintained if certain rules concerning the approximation of the
geometric quantities are followed and the contravariant flux components are chosen
as primitive variables, and the grid is not too non-smooth. Good results are
obtained for 2D laminar flows on fairly smooth grids.
In this paper a finite volume method for turbulent flow predictions on staggered
grids in complex geometries employing the contravariant flux components as
dependent variables is presented. Turbulence is modeled by the standard high-Re
k- model with wall functions. The discretization incorporates central
differences for the momentum equations and hybrid central/upwind differences for
the turbulence equations. Accurate approximation of production of turbulent energy
(defined in (2.13)) is obtained. The method is applied to some complex 2D
turbulent recirculating flows, namely driven cavity flow, flow over a backward
facing step, constricted tube flow and flow through an U-bend.
model with wall functions. The discretization incorporates central
differences for the momentum equations and hybrid central/upwind differences for
the turbulence equations. Accurate approximation of production of turbulent energy
(defined in (2.13)) is obtained. The method is applied to some complex 2D
turbulent recirculating flows, namely driven cavity flow, flow over a backward
facing step, constricted tube flow and flow through an U-bend.



Next: Equations governing incompressible
Up: Finite volume computation of
Previous: Finite volume computation of
ISNaS ontwikkeling
Fri May 26 14:01:30 METDST 1995
 model is the most prominent. This model consists of two transport equations for
the turbulent kinetic energy k and its dissipation rate
model is the most prominent. This model consists of two transport equations for
the turbulent kinetic energy k and its dissipation rate  . Both equations
contain a quantity
. Both equations
contain a quantity 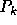 called the production rate of turbulent energy. In the
coordinate-invariant approach this quantity contains Christoffel symbols (in 2D
eight different Christoffel symbols occur). Hence, it seems attractive to
implement the k-
called the production rate of turbulent energy. In the
coordinate-invariant approach this quantity contains Christoffel symbols (in 2D
eight different Christoffel symbols occur). Hence, it seems attractive to
implement the k- model with the Cartesian approach.
model with the Cartesian approach.
 model
has become very popular and has been widely used over the last 15 years
[Habib and Whitelaw, 1982], [Rhie and Chow, 1983], [Peric, 1985],
[Chen and Patel, 1989], [Deng, 1989], [Piquet and Queutey, 1990],
[Lien and Leschziner, 1991], [Cho and Fletcher, 1991], [Melaaen, 1991],
[Coelho and Pereira, 1992], [Zhu and Rodi, 1992], [Xu et al., 1993],
[Rolfes et al., 1993] and [Issa and Oliveira, 1994].
model
has become very popular and has been widely used over the last 15 years
[Habib and Whitelaw, 1982], [Rhie and Chow, 1983], [Peric, 1985],
[Chen and Patel, 1989], [Deng, 1989], [Piquet and Queutey, 1990],
[Lien and Leschziner, 1991], [Cho and Fletcher, 1991], [Melaaen, 1991],
[Coelho and Pereira, 1992], [Zhu and Rodi, 1992], [Xu et al., 1993],
[Rolfes et al., 1993] and [Issa and Oliveira, 1994].
 model. The main disadvantage
of this method is that for time-dependent flow problems it is difficult to
obtain accurate mass conservation.
model. The main disadvantage
of this method is that for time-dependent flow problems it is difficult to
obtain accurate mass conservation.
 model in general coordinates are [Rapley, 1985],
[Braaten and Shyy, 1986], [Yung et al., 1989] and [Chen et al., 1990]. It
should be recognized that this approach may give rise to unstable discretizations.
Following Chen et al. (1990), the more common way to avoid this, is to
choose the coordinate system such that the angle between the velocity components
and the grid lines is not too large. However, for special domains it is very
difficult to achieve this, especially in 3D.
model in general coordinates are [Rapley, 1985],
[Braaten and Shyy, 1986], [Yung et al., 1989] and [Chen et al., 1990]. It
should be recognized that this approach may give rise to unstable discretizations.
Following Chen et al. (1990), the more common way to avoid this, is to
choose the coordinate system such that the angle between the velocity components
and the grid lines is not too large. However, for special domains it is very
difficult to achieve this, especially in 3D.
 model are presented in [Pope, 1978], [Rastogi, 1984],
[Demirdzic et al., 1987], [Stern et al., 1988], [Majumdar and Rodi, 1989]
and [Koshizuka and Oka, 1991]. Stern et al. (1988) have formulated the
governing equations in vector notation which has the advantage that Christoffel
symbols do not occur explicitly. Rastogi (1984) and Majumdar et al. (1989)
use contravariant velocity components to solve the Navier-Stokes equations, while
Pope (1978), Demirdzic et al. (1987) and Koshizuka et al. (1991) employ
contravariant physical velocity components as unknowns.
model are presented in [Pope, 1978], [Rastogi, 1984],
[Demirdzic et al., 1987], [Stern et al., 1988], [Majumdar and Rodi, 1989]
and [Koshizuka and Oka, 1991]. Stern et al. (1988) have formulated the
governing equations in vector notation which has the advantage that Christoffel
symbols do not occur explicitly. Rastogi (1984) and Majumdar et al. (1989)
use contravariant velocity components to solve the Navier-Stokes equations, while
Pope (1978), Demirdzic et al. (1987) and Koshizuka et al. (1991) employ
contravariant physical velocity components as unknowns.
 model with wall functions. The discretization incorporates central
differences for the momentum equations and hybrid central/upwind differences for
the turbulence equations. Accurate approximation of production of turbulent energy
(defined in (
model with wall functions. The discretization incorporates central
differences for the momentum equations and hybrid central/upwind differences for
the turbulence equations. Accurate approximation of production of turbulent energy
(defined in (