Limiting discontinuous-Galerkin solutions using wavelets
Thea Vuik
Thesis advisor: Prof.dr.ir. A.W. Heemink
Daily supervisor: Jennifer K. Ryan
Site of the project: TU Delft
start of the project: December 2011
In March 2012 the
Interim Thesis
and a
presentation has been given.
The Master project has been finished in August 2012
by the completion of the
Masters Thesis
and a final
presentation
has been given.
For working address etc. we refer to our
alumnipage.
Summary of the master project:
To efficiently apply discontinuous Galerkin methods (DG) to hyperbolic problems that develop shocks, limiting techniques are used to reduce the spurious oscillations that develop near discontinuities. Addressing the issue of limiting techniques is useful in many areas such as climate modelling, shallow water equations, and computational fluid dynamics. Although there are many standard limiting techniques, there is no consensus on a proper limiting procedure for multi-dimensional calculations.
There are two difficulties in addressing the issue of limiting. One is how to detect the discontinuity itself, especially in multi-dimensions, and the second is how to maintain high accuracy away from the shock.
This project proposes to take advantage of the many degrees of freedom that are evolved in time for DG and implement a multi-resolution analysis (MRA) type idea for limiting the DG approximation. Although this idea is similar to previous procedures in that it modifies the coefficients used in the approximation, it uses techniques from wavelet analysis to do this modification. The ideas will be implemented locally, in regions where limiting is necessary instead of applying the usual total variation bounded (TVB) limiter.
The discontinuous Galerkin method is a promising tool for many as yet unexplored applications but finding a proper limiting procedure is challenging. The value of the proposed research is that by examining the solution space such as non-polynomial and wavelet-type bases in these regions will allow for new developments of limiting procedures for the discontinuous Galerkin method. Additionally, possible benefits of exploring such solution spaces are that it provides another computational resource for improving efficiency for applications in climate modelling, shallow water equations, and computational fluid dynamics.
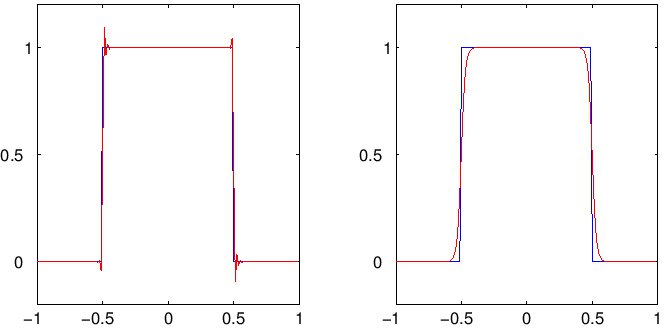
Example of a one-dimensional discontinuous Galerkin (DG) solution (in red) compared to the exact solution (blue) to a linear transport equation with square-wave initial condition. Left: without limiting; Right: with limiting. Without limiting, the DG solution develops spurious oscillations near discontinuities. These limiting techniques can be applied to models for shallow water.

Propagation of waves in the harbor of Zeebrugge, Flanders

Contact information:
Kees
Vuik

Back to the
home page
or the
Master students page of Kees Vuik


![]()
![]()