In 2D, prescribed velocity given means in the present version 
and 
given. These quantities are transformed to
contravariant components using the formulae (6.1) and (6.4) from Van
Kan et al. (1991):
Here the definitions of 
and 
as described above are meant
both for the physical components as for the computational
components.
The given normal velocity component (in computational space) is implemented by
explicitly prescribing the velocity unknown at the boundary. In the program
this is implemented by setting the corresponding main diagonal element
equal to 1 and the off-diagonal elements in the corresponding rows to 0. The
right-hand-side component corresponding to this unknown is made equal to
the unknown itself.
The given velocity component 
is implemented in the following
way:
The matrix is built for all unknowns including all the ''tangential''
unknowns. The rows corresponding to the ''tangential'' unknowns closest to
the boundary (see Figure 7.1) contain elements referring to virtual
pressures and virtual ''tangential'' velocity unknowns.
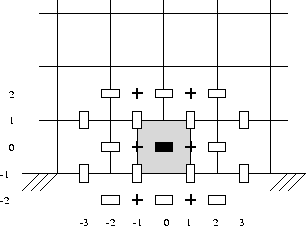
Figure 7.1: A ''tangential'' velocity cell at the boundary
The virtual quantities are expressed in internal unknowns and prescribed velocity components at the boundary using linear extrapolation. For example for the lower boundary (Figure 7.1) we get:
where 
is the value of 
at the boundary
point. The coefficient in the matrix corresponding to the virtual unknown
multiplied by the expression (7.3) or (7.4) is transported
to the right-hand side or the other matrix terms.
