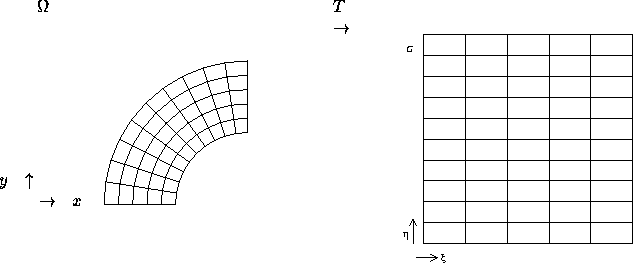
Figure 2.1: Boundary fitted co-ordinates and computational grid
In the ISNaS incompressible code we are dealing with curvilinear boundary fitted grids. These grids are mapped (by an unknown transformation) onto a rectangular computational grid. Figure 2.1 gives a typical example of the mapping from physical (i.e. curvilinear) to computational grid.

Figure 2.1: Boundary fitted co-ordinates and computational grid
All computations are performed in the computational grid and hence the
differential equations are transformed from physical grid to computational
grid. The resulting solution is transformed backwards.
In the sequel we shall use the following notations:

The mapping T from Cartesian to computational domain is given by
We assume that the Jacobian J:
is unequal to zero.
We define the covariant base vector ![]() as the tangent
vector to the surface
as the tangent
vector to the surface ![]() , hence
, hence
The subscript ![]() is placed between parentheses to emphasize that
is placed between parentheses to emphasize that
![]() is not a component but one of the three base vectors
is not a component but one of the three base vectors
![]() .
.
Contravariant base vectors ![]() are defined as normal
vectors to the
are defined as normal
vectors to the ![]() = constant surfaces:
= constant surfaces:
It can be shown that
where ![]() denotes the outer product.
denotes the outer product.
The correspondence between vector and tensor notation for a rank one tensor
is expressed by
For a tensor of rank two the correspondence between the two notations is given by, for example in the case of a mixed tensor:
The covariant and contravariant components of a vector ![]() can be
obtained from
can be
obtained from
For a rank two tensor we have for example