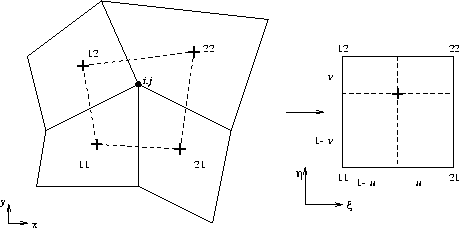
Figure 11.1: Vertex i,j with four surrounding cells and mapping of quadrilateral formed by centroids on to a square.
The scalar unknowns are positioned in the centroids of the cells. In order to interpolate these values to the vertices a weighted mean value of the four surrounding cells is used. Figure 11.1 sketches a typical example.

Figure 11.1: Vertex i,j with four surrounding cells and mapping of
quadrilateral formed by centroids on to a square.
In this figure point i, j is the vertex in which the interpolated values
must be computed. This point is part of 4 cells with centroids 11, 21, 12
and 22. In order to compute the interpolated value, the quadrilateral
spanned by the 4 centroids is mapped onto a unit square (0, 1) ![]() (0,1) by a bilinear mapping as is usual in finite elements.
(0,1) by a bilinear mapping as is usual in finite elements.
So
with ![]()
The value of the scalar in (x, y) is computed by
To evaluate (11.2) it is necessary to know the value of ![]() in point (x, y). This value can be computed from (11.1) by
solving this system of non-linear equation with a Newton-Raphson method.
in point (x, y). This value can be computed from (11.1) by
solving this system of non-linear equation with a Newton-Raphson method.
Define
The Newton-Raphson method can be written as:
![]()
Since Newton is a fast converging process, the maximal number of iterations
is restricted to 5. At this moment the iterations is stopped if ![]() .
.
From (11.3) it follows that:
and
With respect to the boundary points it is not longer possible to use an interpolation. In that case an extrapolation is used. Figure 11.2 shows the four points that are used to compute the value at an under boundary.
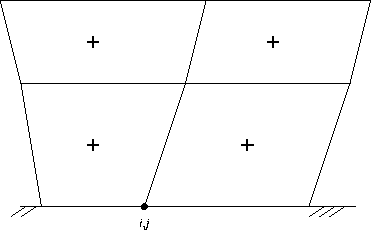
Figure 11.2: Cells that are used to extrapolate the scalar value at the under
boundary i,j.