
The spatial discretization yields systems of ordinary differential equations of the following form:

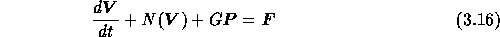
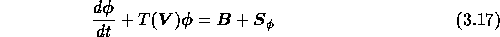
where 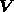 ,
, 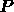 and
and 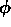 denote
algebraic vectors containing the velocity, pressure and scalar unknowns,
respectively. Furthermore, D and G are the discretized divergence and gradient
operators, N and T represent the discretization of convection and diffusion
terms,
denote
algebraic vectors containing the velocity, pressure and scalar unknowns,
respectively. Furthermore, D and G are the discretized divergence and gradient
operators, N and T represent the discretization of convection and diffusion
terms, 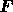 contains the discretized source term and boundary
values,
contains the discretized source term and boundary
values, 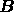 represents a right-hand side term arising from the
boundary conditions and
represents a right-hand side term arising from the
boundary conditions and 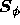 contains the source term which is a
function of
contains the source term which is a
function of 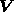 and
and 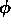 . Time discretization takes
place with the implicit Euler method. Linearization of nonlinear terms is carried
out with the standard Newton method:
. Time discretization takes
place with the implicit Euler method. Linearization of nonlinear terms is carried
out with the standard Newton method:
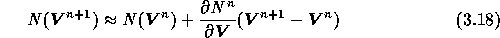
and
For both the k and  equations the inequalities
equations the inequalities
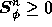 and
and
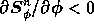 hold,
which preserves positivity of the solutions. For a derivation see [Zijlema, 1993].
The resulting systems of linear equations are solved by a Krylov subspace method
of GMRES type [Saad and Schultz, 1986] with preconditioning. This method is very
suitable for non-symmetric matrices, has a relatively good rate of convergence,
and is vectorizable to a satisfactory degree. For more details we refer to
[Vuik, 1993]. Most authors, like Rapley (1985), Demirdzic et al. (1987),
Majumdar and Rodi (1989), Melaaen (1991) and Coelho and Pereira (1992) adopted
more slowly convergent iterative methods for solving the momentum and turbulence
equations, of which the line Gauss-Seidel method and the strongly implicit method
of Stone (1968) are the most prominent. Both iterative methods are only partly
vectorizable.
hold,
which preserves positivity of the solutions. For a derivation see [Zijlema, 1993].
The resulting systems of linear equations are solved by a Krylov subspace method
of GMRES type [Saad and Schultz, 1986] with preconditioning. This method is very
suitable for non-symmetric matrices, has a relatively good rate of convergence,
and is vectorizable to a satisfactory degree. For more details we refer to
[Vuik, 1993]. Most authors, like Rapley (1985), Demirdzic et al. (1987),
Majumdar and Rodi (1989), Melaaen (1991) and Coelho and Pereira (1992) adopted
more slowly convergent iterative methods for solving the momentum and turbulence
equations, of which the line Gauss-Seidel method and the strongly implicit method
of Stone (1968) are the most prominent. Both iterative methods are only partly
vectorizable.
The overall solution algorithm can be summarized as follows: first, the
continuity equation and the momentum equations are solved. To ensure a
divergence-free velocity field a second order pressure-correction method as
described by Van Kan (1986) is used. Details can be found e.g. in
[Segal et al., 1992]. Finally, the equations for k and  are solved
in a decoupled way. Time-stepping is repeated until a stationary solution is
obtained.
are solved
in a decoupled way. Time-stepping is repeated until a stationary solution is
obtained.