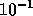 can
be used instead of IBLUD.
can
be used instead of IBLUD.
The main reason for this model study was to reduce the computing times observed with the domain decomposition algorithm for the Navier-Stokes equations, see [4]. This report shows, that it is possible to reduce computing time of the domain decomposition method by a factor 2 to 6 depending on the problem. Specifically, we can reduce computing time to almost that of the single block solution.
As the subdomain solution accuracy is lowered, the number of iterations required to solve the problem remains constant or shows only a small increase, which leads to a reduction in total computing time in our experiments. The most impressive reduction is obtained if the subdomain solution is approximated by an incomplete LU factorization. In this case, we can reduce computing time to almost that of the single block solution. This is an important practical observation, since this makes efficient domain decomposition available for complex problems, for which parallel implementation is not readily available, possible or feasible.
The experiments show that with the Gauss-Seidel version of the IBLUD preconditioner, the number of iterations required for multi-block problems is approximately if not exactly the same as that for single-block solution with ILUD postconditioning. The only reason why there is an increase in computing time when more subdomains are used is overhead by the implementation. This overhead is only noticeable for a large number of relatively small subdomains.
The experiments show that with the algorithm for accurate solution of of subdomains, the solution is sensitive to the subdomain solution accuracy, see Table 2. The GCR based algorithm described in this paper is completely insensitive to the subdomain solution accuracy.
Inaccurate solution of subdomains is also interesting for parallel
implementation. With parallel implementation, however, the IBLUD
postconditioning is preferable. This is because the IBLUD postconditioned
algorithm is more efficient than the algorithm with GMRES solution of
subdomains. Also, the IBLUD postconditioner shows the smallest increase
in iteration count when going from the sequential algorithm to the
parallel algorithm. When communication is a real bottleneck, the
algorithm using a small subdomain solution accuracy of 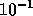 can
be used instead of IBLUD.
can
be used instead of IBLUD.
The new methods investigated in this report will be implemented in the near future for the incompressible Navier-Stokes equations. The efficient implementation of restarted GCR discussed in [25] will be used for that purpose. The current parallel implementation for the Navier-Stokes equations, which uses accurate solution of subdomains, will probably be surpassed by these new methods on a single machine.