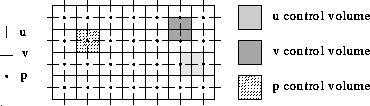
Figure 1: Arrangement of unknowns in a staggered grid
For the spatial discretization, we use a finite volume method employing a staggered grid and central discretization. The normal velocity components are located at the centers of the faces of the cell and the pressure unknowns are located at the centers of the cells, see Figure 1.

Figure 1: Arrangement of unknowns in a staggered grid
For the time discretization, the implicit Euler method is used.
With 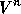 and
and 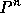 representing the algebraic vectors of velocity and
pressure unknowns at time
representing the algebraic vectors of velocity and
pressure unknowns at time 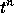 , we get
, we get
where (1) represents the momentum equations and (2)
represents the incompressibility condition 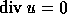 .
The matrix M represents the linearized spatial discretization of the
Navier-Stokes equations around time level
n, G is the discretized gradient operator and D is the discretized
divergence operator on a staggered grid.
Figure 2 shows the discretization stencils.
.
The matrix M represents the linearized spatial discretization of the
Navier-Stokes equations around time level
n, G is the discretized gradient operator and D is the discretized
divergence operator on a staggered grid.
Figure 2 shows the discretization stencils.
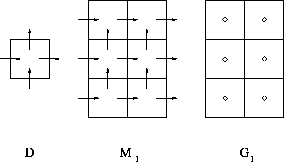
Figure 2: Discretization stencils: discretization of divergence operator D,
x-component of momentum equations 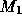 and x component of
gradient matrix
and x component of
gradient matrix 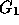 .
.
The pressure correction method [29,16,47]
is used to solve (1) and (2).
The pressure correction method consists of three steps.
In the first step, an estimate 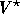 of
of 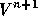 is computed by
solving (1) with the pressure fixed at the old time level:
is computed by
solving (1) with the pressure fixed at the old time level:
In the second step, the pressure correction 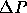 is solved from
is solved from
The last step consists of correcting the pressure: 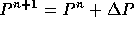 and computing
and computing 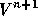 satisfying the incompressibility condition (2)
satisfying the incompressibility condition (2)