
We shall consider flow around a cylinder in a wall-bounded shear flow. This problem models the removal of particles from surfaces. Examples of where this type of flow occurs are for instance, the cleaning of surfaces by water jets, vacuum cleaners and contamination of surfaces. An example of the latter is the disposal route of irradiated fuel of nuclear reactors. Therefore this problem is of considerable practical interest. From a numerical point of view it is interesting because it requires a non-orthogonal grid and the results of the computation can be used to verify assumptions made by experimentalists [28,37]. The problem also requires large computing times, about 7 hours on a single workstation, which makes it a challenge for algorithmic improvements and parallel computing.
Figure 5 shows the geometry and decomposition of the domain and a coarse version of the multi-block and single-block grids. Decompositions into more blocks are obtained by further decomposing the two blocks into subblocks.
The cylinder has diameter a = 2. The Reynolds number is defined as

with

where 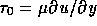 is the shear stress associated with the
linear inlet velocity profile. Typical Reynolds numbers for this problem
are
is the shear stress associated with the
linear inlet velocity profile. Typical Reynolds numbers for this problem
are 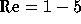 . Our results are given for
. Our results are given for 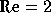 .
In the computation we have used L = H = 10.
The boundary conditions are as follows:
.
In the computation we have used L = H = 10.
The boundary conditions are as follows:
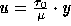 , v = 0
, v = 0
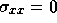 , v = 0
, v = 0
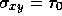 , v = 0
, v = 0 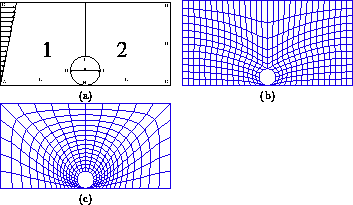
Figure 5: (a) Geometry and decomposition of the domain.
(b) multi-block grid
(c) single-block grid
The stationary solution is computed using the implicit Euler time integration
scheme with start time t = 0, end time t = 10 and with time step 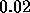 .
The time measurements in the next section
are given for only the first 10 time steps to avoid
excessive computing times. Figure 6 shows the streamlines for
the stationary solution. For more details on this computation,
the reader is referred to [10].
.
The time measurements in the next section
are given for only the first 10 time steps to avoid
excessive computing times. Figure 6 shows the streamlines for
the stationary solution. For more details on this computation,
the reader is referred to [10].

Figure 6: Streamlines of the stationary solution