Mesh Generation in Underground Layers Near Faults (
figuren)
Abdelkader Hajjaoui
Plaats van afstuderen:
Shell Research
Volmerlaan 8
2280 AB Rijswijk
start van afstuderen: september 1997
De afstudeeropdracht is mei 1998 afgerond met het schrijven van het
afstudeerverslag.
Korte omschrijving van de afstudeeropdracht:
Shell is one of the major oil companies, serving customers in most of
the countries of the world.
The main activities are exploring for hydrocarbons (oil and gas),
production of oil and gas from
the reservoirs in the earth, refining the crude oil into products and
selling these.
In SIEP-EPT technical advice and research is carried out for the
Shell companies involved
in exploration and production of hydrocarbons for reservoirs.
Within SIEP-EPT, the HM ( Hydrocarbon systems Modeling)
group has the task to add value to
Shell's business by providing integrated solutions to basin-scale
geological problems.
Hydrocarbon systems Modeling involves the physical description of a
sedimentary basin in space and geological time.
This means that one tries to describe how the basin was formed, and how
the sediments and pore
fluid, including hydrocarbons, were generated and migrated.
Insight in the forming of hydrocarbons and how they moved is essential
in deciding where search for hydrocarbons reservoirs.
The current areas of direct application to exploration are :
- Calculation of source rock temperature histories for use in
hydrocarbon generation.
- Hydrocarbon generation.
- Migration of hydrocarbons from source rocks to reservoir rocks.
- Overpressure for safe and cost effective drilling strategies.
The HM group uses mathematical models as powerful techniques for
resolving temperature problems
and overpressure problems in underground layers.
In general, the mathematical model of earth processes is based on the
conservation of the basic
properties involved e.g heat,mass and momentum.
The description of all these processes result in a coupled system of
partial differential equations.
Such equations have only a unique solution when a series of boundary and
initial conditions are
imposed.
In general, the applicability of analytical methods is limited to
problems with configurations
of simple shape and composition. In practice, however, we are often
confronted with complex geometries
and with non linear terms.
Due to the availability of high-speed, large-capacity digital computers,
numerical techniques play an
increasing important role in earth process calculations.
The main advantage of these techniques is their general applicability:
they are flexible with regard
to shape, size and physical composition of different geometrical
constituents that together form
the configuration that one wants to analyze.
The numerical techniques are based on a discretization of the equations
governing the relevant
physical processes, as the temperature and overpressure modelling. To
solve the partial differential
equations, discretization techniques are used. For simple geometries
one usually applies finite
difference methods, but if the region becomes more complex, finite
element methods are more flexible.
In sedimentary basins, faults act as both seals and conduits for fluid
flow.
Processes such secondary migration , temperature distribution and
overpressure development
depend critically on the fault pattern.
In the present Shell program that is used to predict temperature and
overpressures in a geological
setting, a finite element mesh is used, which consists of four node
quadrilaterals in two dimensions,
and of eight node hexahedrons in three dimensions.
The grid generator does not take into account where the faults are. As a
consequence
very undesirable meshes will be generated.
It is the aim of this research to adapt this finite element mesh such
that acceptable meshes
necessary for the computations arises.
The mesh generator must satisfy certain requirements :
- Quality to ensure reasonable element shapes and to control
element size.
- Efficiency with regard to computational time and memory. Further
the present mesh must be kept
as much as possible for these parts at a certain distance of the
fault.
- A correct representation of discontinuities in the underground
layer see Figure 1.
- Tetrahedra elements must be used.
An additional feature of this grid generator is that it should be able
to handle regions which change
position with geological time.

One horizon and a number of faults
A brief description of how the unstructured grid generation in the
neighborhood of faults will be
developed is as follows:
- Investigate the supplied grids.
- Provide mapping : A piecewise linear mapping is used to
map the fault plane
onto the computational space, where the
structure of the intersection
between horizon and fault node is retained see Figure 2.
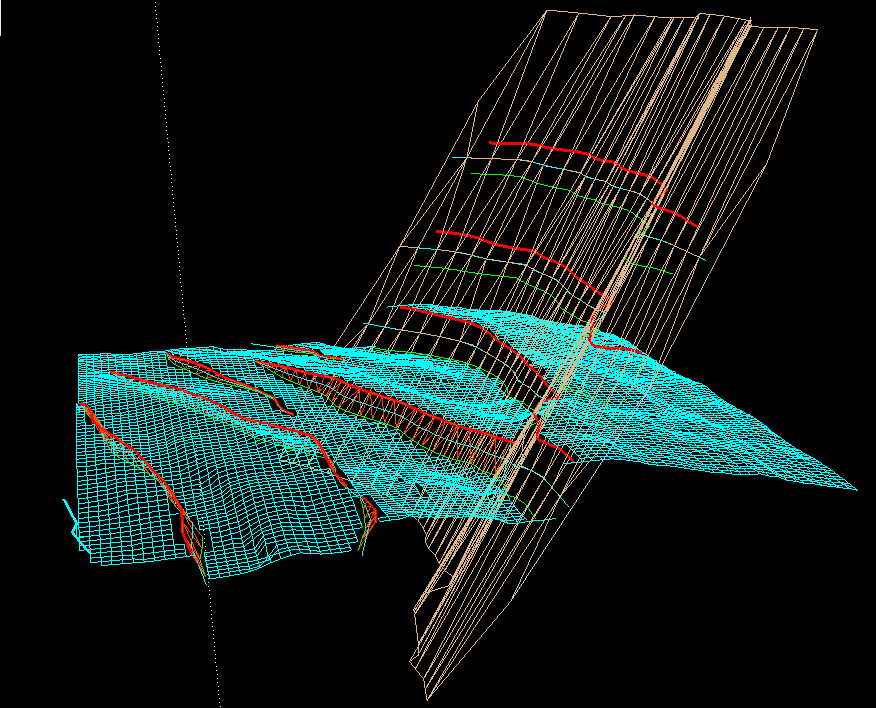
One horizon and the fault plane
- Creation triangulation process : The triangulation of the
fault plane will be applied in
the computational space in such way that :
- The intersection line of the horizon grids and the fault plane
must be part of the grid after
creation of the unstructured triangular elements see Figure 3.
And some node points which
represent the intersection between some grid plane and the fault
plane must be part of the grid.

Two horizons and the fault plane
- The inverse mapping : The inverse of the linear mapping is
used to construct
the fault plane in three dimensions from the two dimensional surface
in the computational space.
- Create tetrahedral mesh : The triangulated fault plane in
three dimensions is extended to a
domain with tetrahedral elements in such a way that :
- The fault plane must be represented by one surface grid. The
fault plane must be present in
the three dimensional mesh.
- Connect hexahedron elements with tetrahedron elements : The
unstructured tetrahedral
meshes in three dimensions will be connected to the hexahedron
tetrahedral mesh at a certain
distance from the faults.
Back to
home page
or
Afstudeer pagina
of Kees Vuik



