The discretization of the transport equation (5.1) as explained in the
previous section is restricted to more or less smooth grids. Moreover,
the diffusion coefficient ![]() often varies rapidly, so that
often varies rapidly, so that
![]() has large jumps on cell faces. Hence, straightforward
discretization
of the diffusivity may results in large errors even on smooth grids. Here we shall
consider a discretization which is exact for uniform and linear scalar fields,
regardless the smoothness of the grid and of the diffusion coefficient.
For this purpose, we need an expression for the partial derivative of any quantity
has large jumps on cell faces. Hence, straightforward
discretization
of the diffusivity may results in large errors even on smooth grids. Here we shall
consider a discretization which is exact for uniform and linear scalar fields,
regardless the smoothness of the grid and of the diffusion coefficient.
For this purpose, we need an expression for the partial derivative of any quantity
![]() with respect to
with respect to ![]() in terms of general coordinates, namely
in terms of general coordinates, namely
This can be derived using the chain rule and (2.27). We start with the equation (5.1), viz.,
![]()
and with (5.7) taken into account, the appropriate form of the transport equation becomes
Discretization of (5.9) is obtained by integration over a finite
volume ![]() with center (i,j,k).
Hence, we have
with center (i,j,k).
Hence, we have
whereas the time derivative and the source terms are integrated using the midpoint rule:
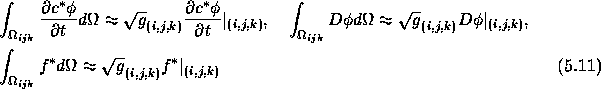
So far, no difficulties arose because none of the quantities used in the above
formulae are discontinuous. Furthermore, these discretizations are second order
accurate and (5.10) is exact for constant ![]() .
The cell-face values have to be approximated in terms of values of
.
The cell-face values have to be approximated in terms of values of ![]() in
neighbouring cell centers by means of interpolation. This will be discussed in
the next section.
The only point left to discuss is the approximation of the diffusion term.
First, for the sake of easier manipulations, the diffusion term will hereafter
be expressed as
in
neighbouring cell centers by means of interpolation. This will be discussed in
the next section.
The only point left to discuss is the approximation of the diffusion term.
First, for the sake of easier manipulations, the diffusion term will hereafter
be expressed as
![]()
Integration over ![]() yields:
yields:
The physical quantity ![]() is everywhere continuous for
arbitrary mappings. Hence, when k is
discontinuous,
is everywhere continuous for
arbitrary mappings. Hence, when k is
discontinuous, ![]() is discontinuous. Thus, approximation of
is discontinuous. Thus, approximation of
![]() using central differences is inaccurate. However, using the
integration-path method an accurate approximation of
using central differences is inaccurate. However, using the
integration-path method an accurate approximation of
![]() at point (i+1/2,j,k), for example, is obtained:
at point (i+1/2,j,k), for example, is obtained:
where
where C is given by
and
![]()
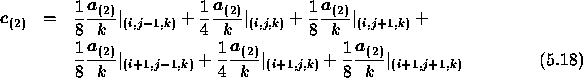
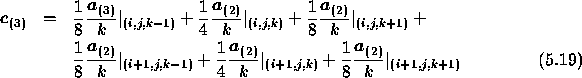
We hereby assume that ![]() .
The two-dimensional version of (5.15) and (5.16) are given by
.
The two-dimensional version of (5.15) and (5.16) are given by
![]()
with
![]()
Substitution of (5.14) in (5.13) gives a discretization which
is exact when ![]() is constant, and hence exact for linear scalar fields.
The other cell-face fluxes can be derived in exactly the similar way.
is constant, and hence exact for linear scalar fields.
The other cell-face fluxes can be derived in exactly the similar way.