In this section we discuss several methods for expressing a cell-face value of a
scalar in terms of surrounding nodal values. For clarity, the discussion relates
to a uniform infinite staggered grid as depicted in Figure 5.1. For
reasons of robustness and algorithmic simplicity, multidimensional central and
upwind schemes
are treated by one-dimensional decomposition in the normal direction for each
cell face. Such schemes are called splitting schemes. Therefore we restrict
ourselves to interpolation of the face values along one specific direction in
G-space, taking for example the ![]() -direction.
We need to consider only the cell-face value
-direction.
We need to consider only the cell-face value
![]() . The other face values will be treated in the same way.
. The other face values will be treated in the same way.
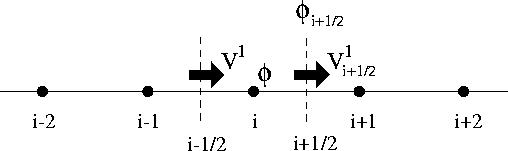
Figure 5.1: One-dimensional staggered grid showing the nodes involved in the
evaluation of ![]() at cell-face
at cell-face ![]() .
.
{
In this scheme, the face value ![]() is approximated by means of linear
interpolation in the following way:
is approximated by means of linear
interpolation in the following way:
resulting in second order accuracy. This scheme is obviously conservative and is not positive when a mesh-Péclet number defined as the ratio of the contributions to the convection and the diffusion exceeds a certain value. For example, when orthogonal grids are employed the scheme may produce wiggles when the mesh-Péclet number given by (see (5.5) and (5.4)):
becomes greater than 1 in magnitude. In the case of skewed grids the expression
for the mesh-Péclet number depends on how the mixed-derivative terms are
approximated. This will be discussed in Section 5.4.
{
The face value ![]() is equal to the upstream node value and, for reasons
of efficient vector coding, can be expressed as follows
is equal to the upstream node value and, for reasons
of efficient vector coding, can be expressed as follows
This scheme is conservative, first order accurate, and unconditionally positive.
However, when the flow direction is oblique to the grid lines this scheme
produces numerical cross-flow diffusion. This may result in a large error in
the solution.
{
In an effort to combine the advantages of both central and upwind schemes
Spalding [28] has proposed the hybrid central/upwind
difference scheme. The approximation to ![]() is given by
is given by
![]()
where ![]() is given by (5.22),
is given by (5.22), ![]() by (5.24) and
s is a switching function depending on the mesh-Péclet number Pe with
by (5.24) and
s is a switching function depending on the mesh-Péclet number Pe with
![]() . With the hybrid scheme the convection terms
are approximated with central differences, unless |Pe| > 1 when a switch to
the first order upwind scheme is applied:
. With the hybrid scheme the convection terms
are approximated with central differences, unless |Pe| > 1 when a switch to
the first order upwind scheme is applied:
![]()
For convergence reasons, a smooth switching function may be used:
This switching function is obtained by requiring that off-diagonal matrix
elements involving convective and diffusive contributions are non-positive,
which is sufficient for suppression of wiggles.
A disadvantage of the hybrid scheme is that in convection-dominated flows
first order upwind is employed everywhere,
irrespective of whether spurious wiggles arise or not.
A number of higher order convection schemes have been embedded in the
computational procedure. Also, a number of classes of flux-limited schemes based
on the TVD methodology will be presented. All may conveniently
be written in a canonical form involving a few scheme-related parameters. To this
end, the face values ![]() are approximated by the first order upwind
scheme, corrected by adding an appropriate anti-diffusive flux controlled by a
limiter. That is,
are approximated by the first order upwind
scheme, corrected by adding an appropriate anti-diffusive flux controlled by a
limiter. That is, ![]() is approximated by
is approximated by
where
![]()
Formula (5.28) opens the possibility to incorporate arbitrary upwind biased schemes in an algorithmically simple way. The most interesting schemes are
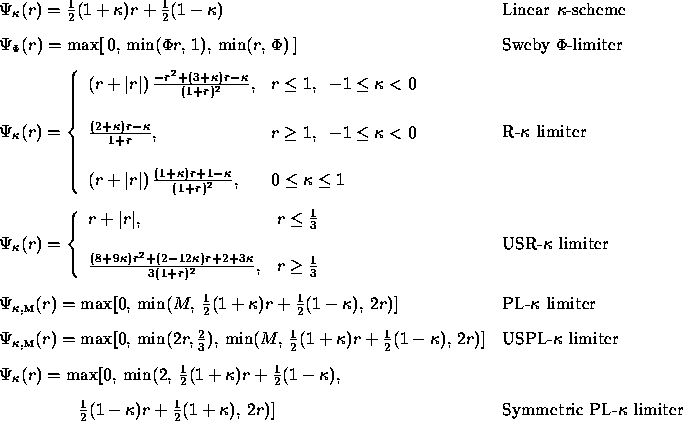
where ![]() ,
, ![]() and
and
![]() .
These classes of flux limiters bring together
most limiters known in the literature. For example,
.
These classes of flux limiters bring together
most limiters known in the literature. For example, ![]() and
and ![]() define the Minmod and Superbee, respectively.
Details can be found in [30, 9]. The functions R-0 and R-
define the Minmod and Superbee, respectively.
Details can be found in [30, 9]. The functions R-0 and R- ![]() are Van Leer [9] and ISNAS [41] limiters. The limited
are Van Leer [9] and ISNAS [41] limiters. The limited
![]() scheme proposed by Koren [13] and SMART scheme
[6] are identical to PL-
scheme proposed by Koren [13] and SMART scheme
[6] are identical to PL- ![]() with M = 2 and PL-
with M = 2 and PL- ![]() with
M = 4, respectively. Finally, by taking
with
M = 4, respectively. Finally, by taking ![]() , M = 2 and
, M = 2 and
![]() , M = 2 for symmetric PL-
, M = 2 for symmetric PL- ![]() limiters the UMIST [16]
and MUSCL [35] schemes are recovered.
Apart from linear
limiters the UMIST [16]
and MUSCL [35] schemes are recovered.
Apart from linear ![]() schemes, USR and USPL limiters, the above classes of
limiters reduce locally to first order accuracy at physical extrema regardless of
the order of accuracy in regions of monotonicity. If USR and USPL limiters are
employed uniform second order accuracy is obtained (
schemes, USR and USPL limiters, the above classes of
limiters reduce locally to first order accuracy at physical extrema regardless of
the order of accuracy in regions of monotonicity. If USR and USPL limiters are
employed uniform second order accuracy is obtained ( ![]() ).
For more details we refer to [42], where further extensive references
can be found.
).
For more details we refer to [42], where further extensive references
can be found.
Generally, the function ![]() is nonlinear, and more than 2 immediate
neighbouring nodal points per spatial direction may be involved in
approximating the convective flux
is nonlinear, and more than 2 immediate
neighbouring nodal points per spatial direction may be involved in
approximating the convective flux ![]() .
Difficulties for iterative solution methods can be
circumvented by writing the flux
.
Difficulties for iterative solution methods can be
circumvented by writing the flux ![]() in
terms of a lower order approximation plus a correction term. This is known as the
defect correction technique and was probably first used in the present
context by Khosla and
Rubin [12]. More specifically, the face value
in
terms of a lower order approximation plus a correction term. This is known as the
defect correction technique and was probably first used in the present
context by Khosla and
Rubin [12]. More specifically, the face value ![]() is written
as
is written
as
where ![]() stands for the approximation by a
lower order scheme, for example, first order upwind, and
stands for the approximation by a
lower order scheme, for example, first order upwind, and
![]() is the higher-order approximation.
The term in brackets is evaluated explicitly using the values from the previous
time step, which is indicated by the superscript `o'. It is
typically small compared to the implicit part, so that its explicit
treatment does not slow down convergence. This approach ensures diagonal
dominance for the resulting algebraic equations, thus enhancing iterative rate of
convergence while restoring higher-order accuracy at steady-state convergence.
The limited anti-diffusive parts of (5.28) may be
viewed as deferred corrections to the first order upwind approximation and hence
can be put into the source term. Since the stencil
associated with first order upwind is maintained, existing codes can
easily be modified.
is the higher-order approximation.
The term in brackets is evaluated explicitly using the values from the previous
time step, which is indicated by the superscript `o'. It is
typically small compared to the implicit part, so that its explicit
treatment does not slow down convergence. This approach ensures diagonal
dominance for the resulting algebraic equations, thus enhancing iterative rate of
convergence while restoring higher-order accuracy at steady-state convergence.
The limited anti-diffusive parts of (5.28) may be
viewed as deferred corrections to the first order upwind approximation and hence
can be put into the source term. Since the stencil
associated with first order upwind is maintained, existing codes can
easily be modified.