In this section we shall focus on schemes for expressing cell-face derivatives (diffusive flux) in terms of neighbouring nodal values. Special attention will be paid to the mixed derivative terms arising from non-orthogonality of the coordinate system, particularly in view of the demand of positivity of turbulence quantities.
Finite volume discretization of the transport equation (5.3) yields equation (5.5). After substituting (5.4) in (5.5) for all cell faces, the following expression for the diffusive flux at cell face (i+1/2,j,k), for example, results:
For convenience we restrict ourselves to the cell-face 
. The
other faces are treated in the same way.
Remark: We assume the mapping 
is smooth, so that
and 
at cell faces may be approximated by bi- or trilinear interpolations in the
obvious way.
If the grid is orthogonal, the last two terms of (5.31)
vanish and the first part is approximated with central differences, as
follows:
and no further approximation is required. Clearly, this approximation is
conservative and contributes to a positive scheme. The local truncation
error is second order. However, when a non-orthogonal grid is
used, the approximation of the mixed derivatives
may cause spurious wiggles. For example, if we approximate
by central differences
and bilinear (4-point) interpolation (required to express the
-values at cell vertices in terms of nodal values) as follows:
then the coefficients corresponding to
and 
get the wrong sign, if
. On the other hand, if 
,
we get negative contributions to the coefficients of 
and
. This does not necessarily result in oscillatory solutions.
In fact, these coefficients are usually small relative to the coefficients
belonging
to the normal derivative 
, but, in some
circumstances, for example when the grid is highly non-orthogonal, they become
significant and wiggles may occur. Since this is undesirable, we shall consider
three methods to address this difficulty.
{
The most obvious approach is to treat the mixed-derivative terms explicitly, i.e.
they are evaluated at the previous time level and are incorporated in the
source term. This method is most frequently used in several numerical procedures.
It reduces the size of the stencil to a 5-point or 7-point one in 2D and 3D,
respectively, and does not lower the order of accuracy in the stationary case.
However, this method may cause serious deterioration in the convergence rate,
particularly when the grid is highly non-orthogonal, and wiggles may still show
up in the steady-state solution.
{
In this method, proposed by Demirdzic [4], 2-point rather than
4-point interpolation is employed. For example, suppose that
, then the following approximation is taken:
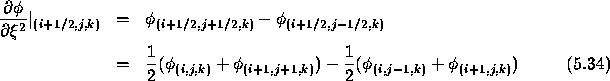
If , we have
This scheme is symmetric around (i+1/2,j,k) and thus second order
accurate. Similar expressions follow for the last term of (5.31).
The scheme is conservative, and produces unconditionally non-negative "corner"
coefficients, i.e. those corresponding to ,
, 
and 
.
But it does not always guarantee positivity, since the
contributions to the "principal" coefficients at points (i,j-1,k), (i+1,j,k),
(i,j+1,k), (i,j,k-1) and (i,j,k+1) can be either positive or negative.
However, the 
terms give contributions to these coefficients of the
correct sign, which dominate if 
is not too large.
All schemes previously considered do not guarantee unconditional positivity
of the scheme.
In what follows, a new scheme that satisfies positivity will be described.
It employs one-sided rather than central differences such that only
non-negative coefficients are involved. The mixed derivative with respect to
at (i+1/2,j,k) is evaluated as follows:
Obviously, this decreases the accuracy to order one, but the scheme is unconditionally positive. Expressions similar to (5.36) follow for the last term of (5.31). Since the cell-face differences are uniquely defined at each cell face, the scheme is also conservative.
