One of the source terms in turbulence model equations is the production rate
of turbulent energy given by (6.9). The discretization of
this term is carried out at center (i,j,k) with central differences and bilinear
interpolations in which the fewest number of neighbouring nodal points are taken.
Since we use 
as unknowns, the covariant derivative
of the contravariant velocity components must be expressed in terms of flux
components. We have
The partial derivative of the flux component can be approximated by central
differences. The same interpolation rules as for the momentum
equations are applied. All geometrical quantities are evaluated at the centre
of a scalar cell. Closest to a boundary, some derivatives
also contain virtual fluxes.
These virtual quantities are expressed in internal fluxes by using linear
extrapolation. In two-dimensional case, for example, at lower boundary we get:
The above discretization is not well-suited when a non-smooth grid is employed.
An approach to discretize the production term in case of non-smooth grids is to
integrate the Cartesian expression of 
over a finite volume 
so that no Christoffel symbols or metric tensors occur in the formulation.
At this moment we restrict ourselves to the Boussinesq hypothesis for the modeling
of the production of turbulent energy. From (6.24) it follows that the
Cartesian expression for is given by
The remain task is to discretize the partial derivatives of the Cartesian velocity
components with respect to 
at point (i,j,k). This can be done
with the integration-path method. Here a "quick" approach is given. To approximate
the 
-derivative of 
this derivative has to be expressed in
terms of the derivative with respect to 
. Using the chain
rule, one gets:
The approximation of (6.33) at point (i,j,k) leads to
Here 
represents the difference in ,
across the cell enclosing point (i,j,k), in 
direction. The
differences are evaluated as:
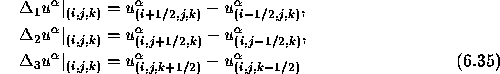
The final expression of the approximation for
becomes
The velocity components on cell faces are to be obtained with
Since 
is only given at center of cell faces, discontinuous
geometric quantities and fluxes have to be replaced by suitable definitions
such that (6.38) is exact for constant on arbitrary
grids. An example:
with
