The normal and tangential stress components at the boundary are prescribed.
Let 
be the normal stress component at the boundary and 
the tangential stress component in the 
direction (see
Figure 7.4). So:
where 
is an unit normal vector and is an unit
tangential vector. From 
and 
we
compute 
and 
the
stresses in the computational domain.
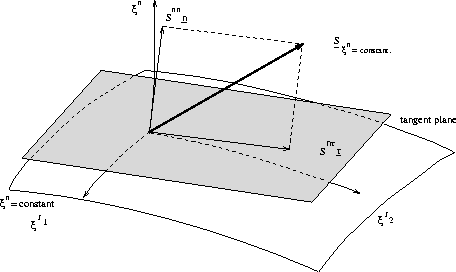
Figure B.1: The normal and tangential stress in the physical domain at the
boundary 
.
Just asin the 2D-case is:
and are computed by:
where
The stress 
is defined by 
. At the boundary it is impossible
to separate the pressure from te deviatoric stress tensor 
. So the discretization of the pressure at the boundary will be
different from the one in the inner region.
We have to consider three different cells closest to the boundary two
''tangential'' and one ''normal'' velocity cell.
Let us first consider the ''tangential'' cells. The two ''tangential''
cells closest to the boundary are considered differently from the ones in
the inner region, because the stencil contain virtual unknowns (see
Figure 7.5).
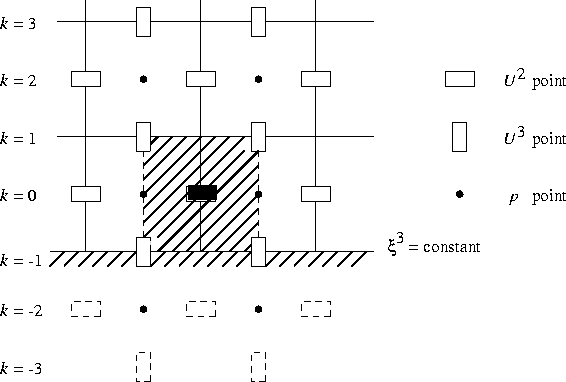
Figure 7.5: A cross-section ( 
) over an
-cell closest to the bottom of the region.
The discretization of the convective terms, the right-hand side and the time derivative are the same as for the inner cells, with the exception that virtual velocities are eliminated by linear extrapolation. For example for the bottom boundary (see Figure 7.5) we get:
The stress tensor is discretized in the following
way for the 
-cell:
Term 
is given by formula (7.23), if
we are concerned with the bottom boundary. All other terms are treated in
the usual way.
Since no normal velocity components are prescribed at the boundary we have
to consider a finite volume around a ''normal'' velocity point at the
boundary (see Figure 7.6).
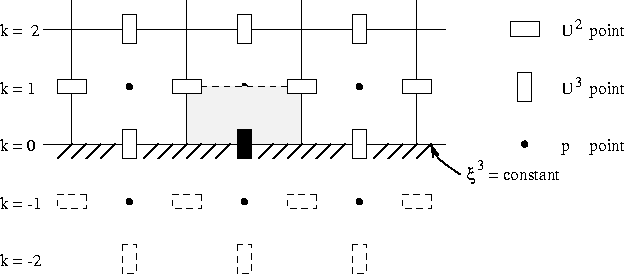
Figure 7.6: A cross-section ( ) over an
-cell at the bottom.
We will now consider the discretization for a ''normal'' velocity cell at the
bottom boundary.
The discretization of the time-derivative gives:
and of the right-hand side:
The discretization of the convective terms is given by:
and the approximation:
If 
or 
are not present at (i,j,1) then they are
approximated by:
The discretization of the stress tensor at the boundary is given by the following formula:
or
where RHS is given by:
The evaluation of 
and
introduces some difficulties. First we need the
pressure in point (0,0,0), because we have to split up 
and 
. Instead of 
we use 
just as in the 2D-case.
Secondly we need 
and
at (0,0,0) for 
. The derivatives 
and
are replaced respectively by
and 
.
In Van Kan et al. (1991), page 34, there are three
strategies mentioned to compute 
and 
. It seems reasonable if we use the same strategy as
used in the 2D-case. That is, the derivatives and are computed at the preceding time level, 
and at
the boundary are computed by linear extrapolation, using two points, so:
(at the preceding time level) for 
.
