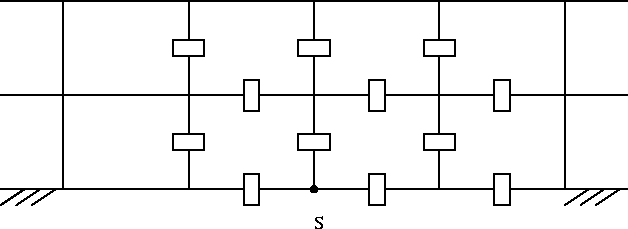
Figure 7.7: transition point S (vertex of cell). At the left of point S the type of boundary condition differs from the one on the right.
Just as in the preceding cases we restrict ourselves to the lower boundary in the computational domain. Let at the vertex point S we have two types of boundary conditions (see Figure 7.7).

Figure 7.7: transition point S (vertex of cell). At the left of point S
the type of boundary condition differs from the one on the right.
We shall only consider the
boundary condition at the left of point S but in relation to the boundary
condition at the right. In all cases the most restrictive boundary
conditions, i.e. the one that influences the velocity most directly will be
applied. Let us first consider Dirichlet boundary conditions at the left of
S. Since Dirichlet boundary conditions are the most restrictive, it is
assumed that also in point S the velocity is prescribed. All points
left of S are treated in the usual way. The only special treatment is
required for the tangential cell just above point S
(Figure 7.8).
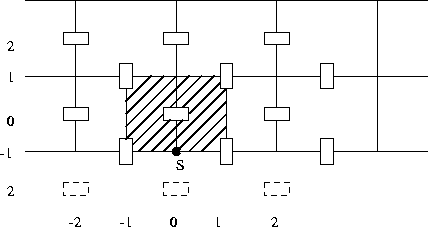
Figure 7.8: Tangential cell just above transition point S.
The molecule corresponding to ![]() contains 3 virtual points, 2
of which can be eliminated by linear extrapolation using the boundary
conditions.
contains 3 virtual points, 2
of which can be eliminated by linear extrapolation using the boundary
conditions.
The only special point is ![]() . If at the right side of S we
have a boundary condition of type 3 this point may be treated in the usual
way. However, if boundary conditions of type 2 or 4 are prescribed
. If at the right side of S we
have a boundary condition of type 3 this point may be treated in the usual
way. However, if boundary conditions of type 2 or 4 are prescribed
![]() must be eliminated by the linear extrapolation:
must be eliminated by the linear extrapolation:
Now suppose that we have a boundary condition of type 2 at the left side of S and a boundary condition of type 1, 3 or 4 at the right side of S. It is sufficient to consider the tangential cell sketched in Figure 7.8 and the normal half cell left of point S sketched in Figure 7.9.
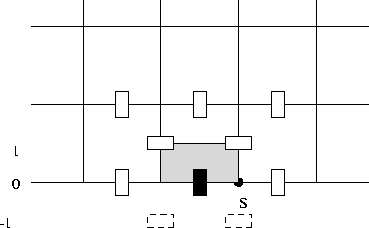
Figure 7.9: Normal half cell left of the transition point S
All other cells are treated in the usual way. Let us first consider the
tangential cell of Figure 7.8. If at the right side of point S we
have a boundary condition of type 1 or type 3, the tangential velocity in
point S is given and the cell is treated as if corresponding to the right
side. In the case of boundary conditions of type 4 the cell may be treated
in the usual way.
With respect to the normal half cell we can proceed as usual. Since no
virtual velocities appear no special treatment is necessary.
In the case that we have a boundary condition of type 3 at the left side of
S we also distinguish between the tangential cell of Figure 7.8
and the normal half cell of Figure 7.9. With respect to the
tangential cell the procedure described in 5.3.1 can be applied without any
restriction. With respect to the normal half cell we may also proceed in
the standard way, i.e. apply formula (7.42). This procedure leads
to virtual unknowns which may be eliminated in the usual way. There is no
need to use extra information if velocities are given at the right of point
S.
Finally with respect to boundary conditions of type 4 it is sufficient to
consider the tangential cell of Figure 7.8. If at the right side of
point S boundary conditions of type 1 or type 3 are given (i.e. ![]() prescribed) these boundary conditions prevail. In the case of boundary
condition of type 2 at the right side of S, no special action is
necessary.
prescribed) these boundary conditions prevail. In the case of boundary
condition of type 2 at the right side of S, no special action is
necessary.