We have to prove (see Figure A.1):
and
where
and
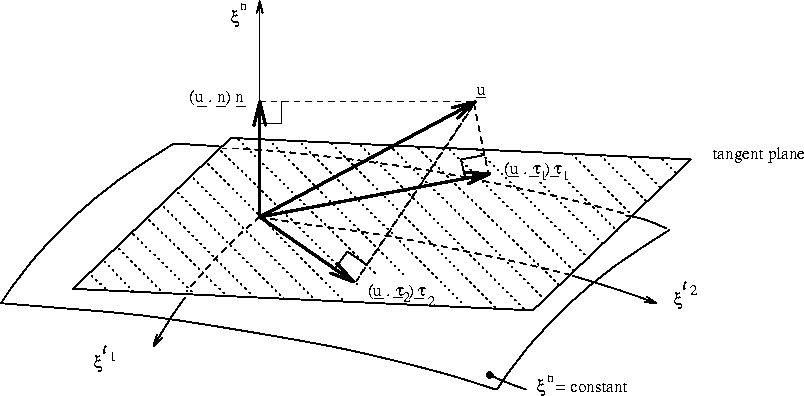
Figure: Normal and tangential velocity components are given by the user
( 
)
First (A.1):
so
This formula is true if 
and 
have the same direction
else we have to use:
Formula (A.2):
The tangential vector 
, given by the user can be decomposed
in the following way:
see Figure A.2.
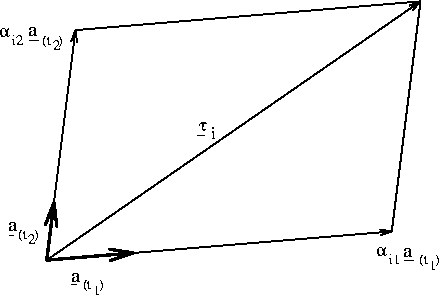
Figure A.2: Decomposition of 
.
The calculation of 
:
From Figure A.2 it is clear that
and
Frome (A.6), (A.7) and Cramer's rule we obtain.
and
Back to formula (A.5):
so:
Formula (A.11) and (A.12) in matrix notation gives:
or:
Hence:
where is given by (A.8) and (A.9).
