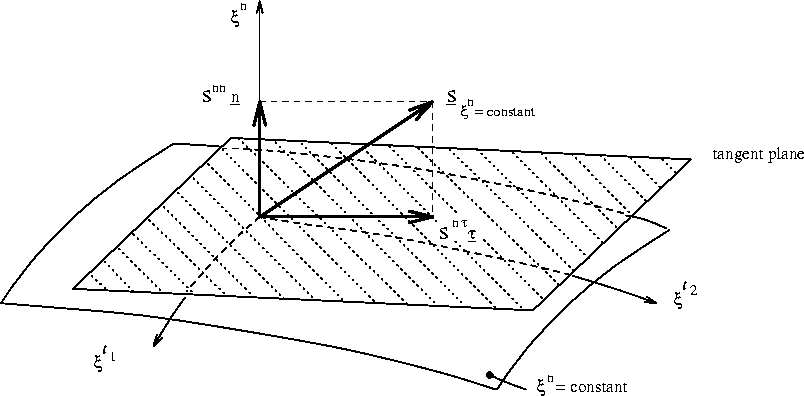
Figure: The normal and tangential stress in the physical domain at the boundary
We have to prove (see Figure B.1):

Figure: The normal and tangential stress in the physical domain at the
boundary ![]() .
.
and
where
We start with formula (3.17) from [11]:
where ![]() is stress tensor in the physical domain.
is stress tensor in the physical domain.
From ![]() and (B.5) we get:
and (B.5) we get:
so
It should be noticed that ![]() and
and ![]() are not tensors.
are not tensors.
The normal vector ![]() pointing in the outside direction of the domain
is equal to:
pointing in the outside direction of the domain
is equal to: ![]() if
if ![]() is
pointing in the outside direction and
is
pointing in the outside direction and ![]() otherwise. Formally we can write:
otherwise. Formally we can write:
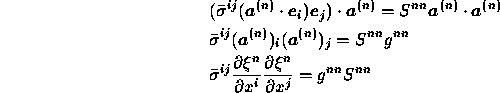
so
![]()
![]()
Formula (B.2):
The tangential vector ![]() is just as in the previous proof equal
to:
is just as in the previous proof equal
to:
where
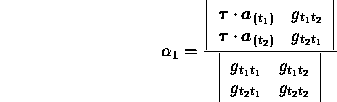
and
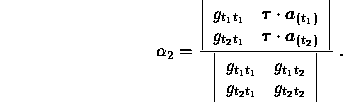
From (B.7), (B.8) and (B.9) it follows that:
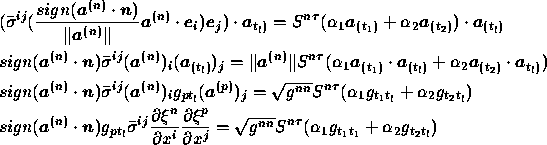
so:
where ![]() is the stress tensor in the computational
domain. For l = 1, 2 we get:
is the stress tensor in the computational
domain. For l = 1, 2 we get:
![]()
and
![]()
or:
![]()
so:
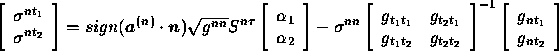
hence:
By using Cramers rule in formula (B.11) we get:
where
and
![]()