


Next: Prospects for parallel
Up: Results
Previous: Lowering the subdomain
One of the main reasons for investigating inaccurate solution of
subdomains was to reduce the excessive computing times observed
in the multi-block incompressible Navier-Stokes solver [4],
and to bring them closer to single block block solution. This also
gives better prospects for parallel computing.
It is therefore interesting to compare single block solution times
with multi-block solution times.
Table 3 lists the number of iterations and computing times
for single block solution of a Poisson equation on an 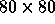 grid.
The results
are given for GMRES subdomain solution using
both ILUD preconditioning and postconditioning.
The postconditioning is a special case of the IBLUD postconditioner
for a single domain. The preconditioner is implemented efficiently
on the level of the subdomain solver.
The first row of the
table thus represents an efficient ILUD preconditioner and the
second row an ILUD postconditioner with some multi-block overhead
(copying of vectors etc.)
grid.
The results
are given for GMRES subdomain solution using
both ILUD preconditioning and postconditioning.
The postconditioning is a special case of the IBLUD postconditioner
for a single domain. The preconditioner is implemented efficiently
on the level of the subdomain solver.
The first row of the
table thus represents an efficient ILUD preconditioner and the
second row an ILUD postconditioner with some multi-block overhead
(copying of vectors etc.)
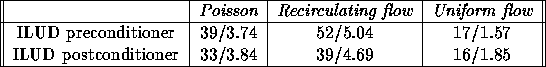
Table 3: Single block solution using GMRES with ILUD pre- and
postconditioning
Table 4 shows a comparison of single block solution
and multi-block solution for the Poisson equation for different
decompositions of the domain.
The decomposition of the domain is indicated as 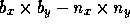 where
where 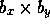 indicates the decomposition into blocks and
indicates the decomposition into blocks and
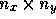 the size of each subdomain in grid cells.
the size of each subdomain in grid cells.
We see that the number of iterations with accurate solution of subdomains
approximately doubles as the same grid is divided up from
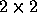 subdomains into
subdomains into 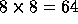 subdomains. As the subdomains are solved less accurate, this increase in
the number of iterations is only slightly less. The IBLU postconditioner
performs well. Although the number of iterations for the same decomposition
of the domain is approximately twice
as much as with GMRES solution of subdomains for the same decomposition
of the domain, the computing time is still
significantly smaller.
subdomains. As the subdomains are solved less accurate, this increase in
the number of iterations is only slightly less. The IBLU postconditioner
performs well. Although the number of iterations for the same decomposition
of the domain is approximately twice
as much as with GMRES solution of subdomains for the same decomposition
of the domain, the computing time is still
significantly smaller.
Note that, despite an increase in the number of iterations,
the computing time is almost constant if
subdomains are solved accurately (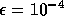 ,
, 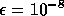 ).
The reason is that subdomain solution
becomes more efficient for smaller problems. This can be seen as follows.
The amount of work required to solve a subdomain problem depends on
the number of unknowns m:
).
The reason is that subdomain solution
becomes more efficient for smaller problems. This can be seen as follows.
The amount of work required to solve a subdomain problem depends on
the number of unknowns m:

with c >0 and 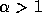 . If the global domain consists of N unknowns
and p subdomains are used, we have
. If the global domain consists of N unknowns
and p subdomains are used, we have 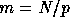 and the
amount of work for one domain decomposition iteration becomes
and the
amount of work for one domain decomposition iteration becomes
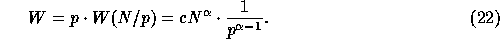
Clearly W decreases as the number of subdomains p rises. Since (21)
is only valid for m large enough, the result (22) is
not valid for large p and computing time will start to increase again.
p.
We see that the number of iterations for IBLUD does not increase
significantly as the number of subdomains is increased. This property is
probably caused by the 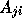 (j > i) terms in the preconditioner
(j > i) terms in the preconditioner
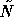 , see Eq. (4),
which were used in the preconditioner. The number of iterations
is almost the same as with single-block solution.
Also, note that for IBLUD postconditioning, the more general GCR acceleration
gives an
overhead of about
, see Eq. (4),
which were used in the preconditioner. The number of iterations
is almost the same as with single-block solution.
Also, note that for IBLUD postconditioning, the more general GCR acceleration
gives an
overhead of about 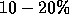 with respect to the more efficient GMRES acceleration.
with respect to the more efficient GMRES acceleration.
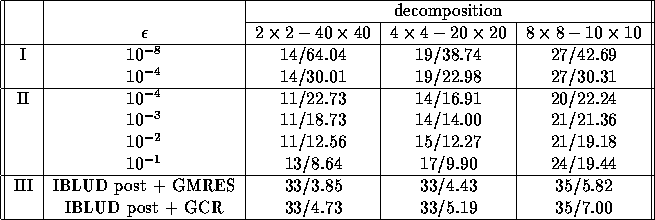
Table 4: Subdivision of the same grid into subdomains for the Poisson
equation. I is the algorithm for accurate solution of subdomains,
II is inaccurate solution of subdomains using GMRES and
III for IBLUD
Table 5 lists the results for the recirculating and
uniform flow problems. Again there is an increase in the number of
iterations as more subdomains are used. With inaccurate solution of
subdomains using GMRES there is an increase of a factor 2 to 3
in the number of iterations for the recirculating flow problem
as the grid is divided into more subdomains. For the uniform flow problem,
this increase is only moderate. With IBLUD postconditioning, the number
of iterations increases only moderately with the number of subdomains.
The number of iterations is approximately equal to that of single
domain solution with ILUD postconditioning, see Table 3,
especially for the uniform flow problem.
This means that, excluding overhead by the implementation, the computing
time should be almost constant as the number of blocks is increased.
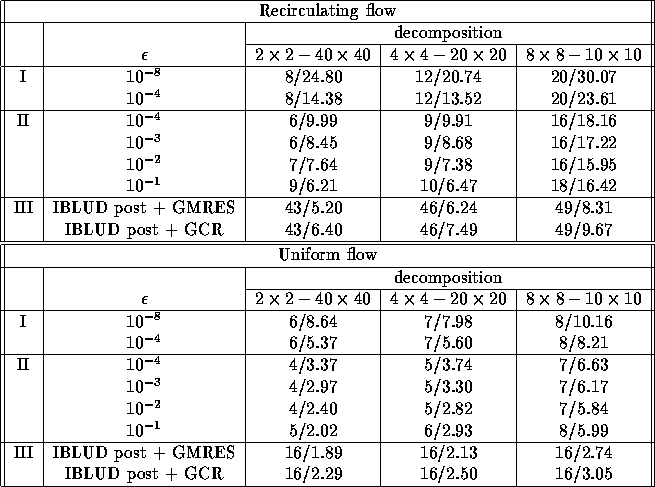
Table 5: Subdivision of the same grid into subdomains for the recirculating
and uniform flow problems.
I is the algorithm for accurate solution of subdomains,
II is inaccurate solution of subdomains using GMRES and
III is for IBLUD
In all three problems, we see that with IBLUD postconditioning, the
GCR based algorithm requires more computing time than IBLUD postconditioning
combined with GMRES. This is what can
be expected because GCR requires more vector updates than GMRES.
Also, as the number of subdomains is enlarged, the number of iterations
with IBLUD does not increase significantly. However, the computing
time still does.
This increase in computing time is caused by overhead of the multi-block
algorithm. Table 6 lists the overhead for solving
the Poisson equation using IBLUD postconditioning with GMRES acceleration.
The computing time is divided into several categories
Categories copy and bc are typical multi-block overhead and
prec and matvec are also present in the single-block case.
The amount of time spent in latter two categories should be approximately
the same for both multi-block and single-block solution.
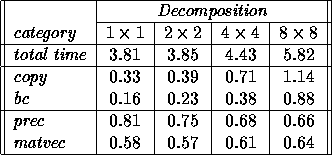
Table 6: Overhead in the multi-block algorithm for inaccurate solution
of subdomains
The overhead in all categories increases significantly as the grid is
subdivided into more domains. The overhead of copying vectors cannot
be easily reduced if we want to retain a black box implementation of
the subdomain solution algorithm. The overhead involved in the
computation of internal boundary conditions can also not be avoided.
As Table 6 shows, the amount of time spent in evaluating
the preconditioner and computing the matrix-vector product is almost
constant as more blocks are used. This is correct, since the number of
iterations stays approximately the same and the global discretization
matrix A is of the same size independent of the number of blocks.



Next: Prospects for parallel
Up: Results
Previous: Lowering the subdomain
ISNaS ontwikkeling
Thu Jun 1 10:46:16 METDST 1995
 grid.
The results
are given for GMRES subdomain solution using
both ILUD preconditioning and postconditioning.
The postconditioning is a special case of the IBLUD postconditioner
for a single domain. The preconditioner is implemented efficiently
on the level of the subdomain solver.
The first row of the
table thus represents an efficient ILUD preconditioner and the
second row an ILUD postconditioner with some multi-block overhead
(copying of vectors etc.)
grid.
The results
are given for GMRES subdomain solution using
both ILUD preconditioning and postconditioning.
The postconditioning is a special case of the IBLUD postconditioner
for a single domain. The preconditioner is implemented efficiently
on the level of the subdomain solver.
The first row of the
table thus represents an efficient ILUD preconditioner and the
second row an ILUD postconditioner with some multi-block overhead
(copying of vectors etc.)
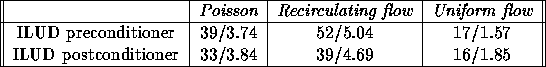
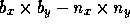 where
where 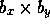 indicates the decomposition into blocks and
indicates the decomposition into blocks and
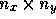 the size of each subdomain in grid cells.
the size of each subdomain in grid cells.
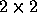 subdomains into
subdomains into 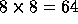 subdomains. As the subdomains are solved less accurate, this increase in
the number of iterations is only slightly less. The IBLU postconditioner
performs well. Although the number of iterations for the same decomposition
of the domain is approximately twice
as much as with GMRES solution of subdomains for the same decomposition
of the domain, the computing time is still
significantly smaller.
subdomains. As the subdomains are solved less accurate, this increase in
the number of iterations is only slightly less. The IBLU postconditioner
performs well. Although the number of iterations for the same decomposition
of the domain is approximately twice
as much as with GMRES solution of subdomains for the same decomposition
of the domain, the computing time is still
significantly smaller.
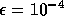 ,
, 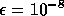 ).
The reason is that subdomain solution
becomes more efficient for smaller problems. This can be seen as follows.
The amount of work required to solve a subdomain problem depends on
the number of unknowns m:
).
The reason is that subdomain solution
becomes more efficient for smaller problems. This can be seen as follows.
The amount of work required to solve a subdomain problem depends on
the number of unknowns m:

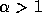 . If the global domain consists of N unknowns
and p subdomains are used, we have
. If the global domain consists of N unknowns
and p subdomains are used, we have 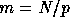 and the
amount of work for one domain decomposition iteration becomes
and the
amount of work for one domain decomposition iteration becomes
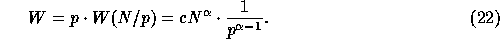
 (j > i) terms in the preconditioner
(j > i) terms in the preconditioner
 , see Eq. (
, see Eq. (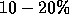 with respect to the more efficient GMRES acceleration.
with respect to the more efficient GMRES acceleration.


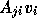 for j>i, see formula (
for j>i, see formula (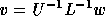 )
(also present with single-block solution)
)
(also present with single-block solution)
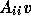 .
.
