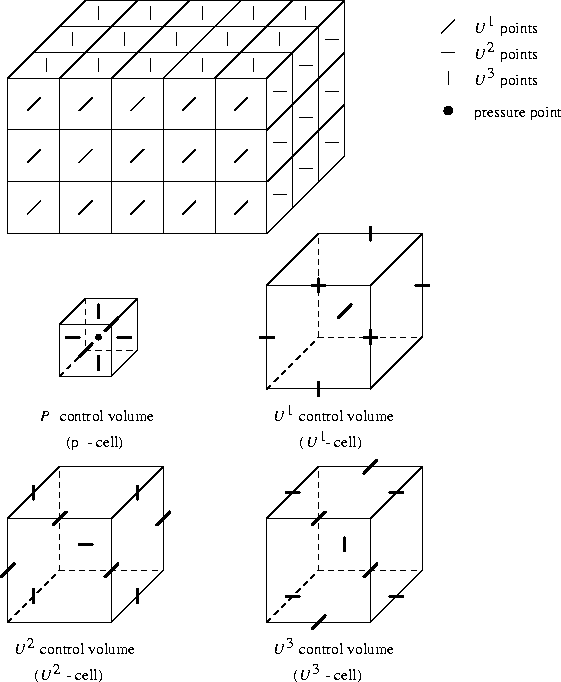
Figure: Arrangement of the unknowns for a staggered grid
First we show in Figure 4.2 the staggered grid arrangements of the unknowns together with the control volumes.

Figure: Arrangement of the unknowns for a staggered grid
If we integrate the continuity equation over a p-cell get
this is a simple extension of formula (4.4).
Just as the 2D-case we splitup the momentum equation. The formulae
(4.5) - (4.14) are all most the same in 3D. The main
difference between 2D and 3D follows from the fact that not a
discretization of formula (4.2) is used but from:
This formula (4.16) follows directly from equation (4.2),
(2.16), (2.21) and ![]() .
.
The discretization of the time derivative is given by:
where (0, 0, 0) is the centre of a ![]() -cell.
-cell.
The discretization of the right-hand-side term is given by
The discretization of the convective terms is given by a straight forward extension of formulae (7.7) and (7.8a)-(7.8b) of Van Kan et al. (1991):
For all non-linear terms in (4.19) we used the Newton linearization given by
where ![]() is taken at the new time level and
is taken at the new time level and ![]() at
the old level.
at
the old level.
Unknowns not present at points where they are required, are computed by
linear interpolation using the fewest number of interpolation
points.
The discretization of the deviatoric stress tensor is carried out according
to:
with ![]() given by formula (4.16).
given by formula (4.16).
The derivatives ![]() in
(4.16) are computed by
central differences, thus:
in
(4.16) are computed by
central differences, thus:
where
![]() is replaced by
is replaced by ![]() . We make here also the
remark that it might be better to replace
. We make here also the
remark that it might be better to replace ![]() by
by ![]() . So use
. So use
instead of formula (4.16) in (4.21).
Finally the discretization of the pressure term is carried out by a
generalization of formula (3.14) in [25]: