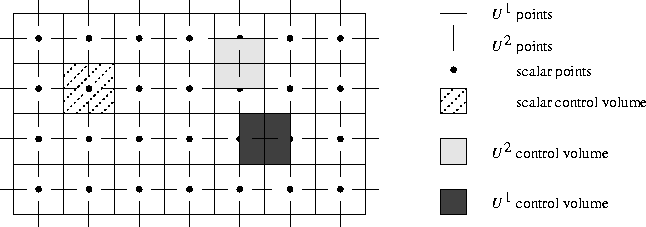
Figure 4.2: Arrangement of the unknowns for a staggered grid
The discretization of the continuity equation is straightforward. We use a staggered grid arrangement as plotted in Figure 4.1.

Figure 4.2: Arrangement of the unknowns for a staggered grid
The continuity equation is integrated
over a so-called pressure-cell. This yields:
where the local numbering of Figure 3.1 is used.
With respect to the discretization of the momentum equations we distinguish
between the time-derivative, the convection term, the pressure gradient,
the deviatoric stress tensor and the right-hand-side term.
The discretization of the time-derivative is given by formula (5.35) of Van
Kan et al. (1991)):
where (0, 0) is the center of a ![]() -cell.
-cell.
The discretization of the right-hand-side term is given by formula (5.34)
of that report:
In order to solve the so-called no flow problem, the discretization of the right-hand side has slightly been improved by taking
![]()
See [26].
The discretization of the convective terms requires a linearization. At
this moment only one type of linearization is available, the Newton
linearization given by
where ![]() is taken at the new time level and
is taken at the new time level and ![]() at
the preceding one.
at
the preceding one.
Apart from the linearization, the discretization of the convective terms is
given by formulae (5.8) and (5.9) of Van Kan et al. (1991):
![]() -cell:
-cell:
![]() -cell:
-cell:
Unknowns not present at points where they are required, are computed by
linear interpolation using the least number of neighbouring points
possible.
The discretization of the deviatoric stress tensor is carried out according
to formulae (5.23) to (5.25) in Van Kan et al. (1991):
![]() -cell:
-cell:
![]() -cell:
-cell:
with ![]() given by formula (2.22) and
given by formula (2.22) and
![]() by formula (4.2).
by formula (4.2).
The derivatives ![]() are
computed by central differences, hence
are
computed by central differences, hence
where for ![]() the local numbering is used.
the local numbering is used.
The same type of interpolation is used as for the convective terms.
![]() is replaced by
is replaced by ![]() in the points where
in the points where
![]() is evaluated, although a better method might be to replace
is evaluated, although a better method might be to replace
![]() by
by ![]() , since
, since
![]() .
.
Finally, the discretization of the pressure gradient is
carried by formula (3.14) in [25]: