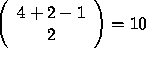We restrict ourselves to the case of boundary conditions at the edge left
under ( 
and 
) in the computational domain. There
are 
possible combinations to prescribe the boundary
conditions, but only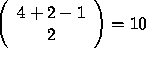 
are really different, see Table 7.1.
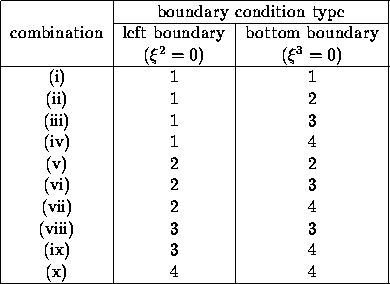
Table 7.1: Combinations of the boundary conditions for the edge left under
( and .)
Since the normal velocities are given at the boundaries we have only to
consider the ''tangential'' 
-cell, see Figure 7.13.
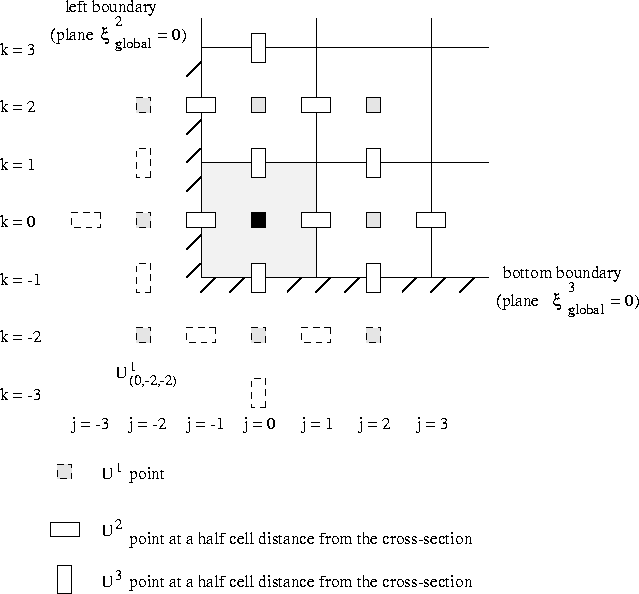
Figure 7.13: Cross-section over the ''tangential'' cell near the edge left
under.
The virtual velocities are eliminated in the usual way
[1]
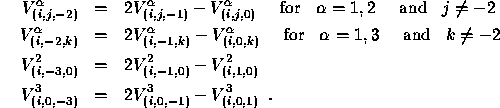
one exception that is for 
. This virtual quantity can be
extrapolated in the following way:
or
Both equations have the same order of accuracy.
Here we have to consider the ''tangential'' cell and the ''normal''
half-cell at the bottom boundary, see Figures 7.13 and 7.14.
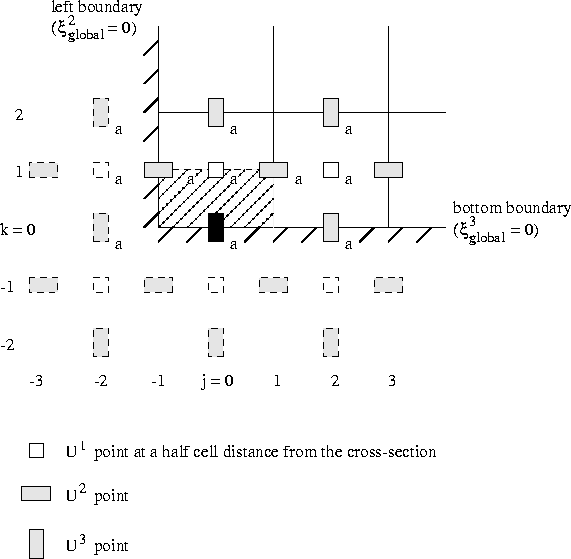
Figure 7.14: Cross-section over a ''normal'' 
half-cell.
''Tangential'' -cell.
The approach is here al most the same as the one prescribed in
paragraph 7.2.2. Although there are more virtual unknowns
they can be eliminated in the usual way. The velocity forms
an exception in this case. We can only use equation (7.67) for the elimination
of , since 
is not prescribed at the bottom
boundary.
''Normal'' half-cell.
Only the velocities marked an a in Figure 7.14 appear in the
discretization, since 
and 
respectively 
and are given at the bottom boundary
respectively left boundary. The approach is almost identical to the one
given in paragraph 7.2.2, only the terms 
and 
are treated in a different way. The
first term is completely known since 
and 
are prescribed at
the left boundary. So this term can be transported to the right-hand
side.
The derivative 
, introduced by the stress
tensor can be computed using the standard elimination rules, so:
where
The and are given at the bottom boundary and
and at the left boundary, so it is necessary to
consider besides the ''tangential'' cell the ''normal''
half-cell.
The ''tangential'' cell can be treated in almost the same way as the
''tangential'' cell in combination (i), see also
paragraph 7.2.2.
The discretization for the ''normal'' half-cell is almost given in
paragraph 7.2.2. But now there are more virtual unknowns and
some of them: 
and
can not be eliminated in the usual way. The virtual unknowns
and 
and (see
Figure 7.14) can be eliminated by using one of the following equations:
for i = -1 or 1,
and
Here we have only to consider the ''tangential'' cell, since the
''normal'' velocities are given ( 
at the left boundary and
at the bottom boundary). For the treatment of the ''tangential'' cell, we
refer to
paragraph 7.4.2. All virtual unknowns (see Figure 7.13)
exept of are eliminated in the usual way. For
we can use formula (7.67).
The stresses 
and 
are prescribed
at the left boundary and and at
the botom boundary. So we have to consider two ''normal' half-cells and the
''tangential'' -cell.
See paragraph 7.2.2, for the treatment of the ''tangential''
cell (Figure 7.15) and the ''normal'' half-cells
(Figure 7.14). However, in this case there are some differences:
Firstly, there are more virtual unknowns, but they caus no extra problems,
since they can be eliminated by using the standard rules.
Secondly, the discretization of the stress tensor 
for the ''tangential'' -cell produces a difference. In formula (7.28) not only
is given, but also 
.
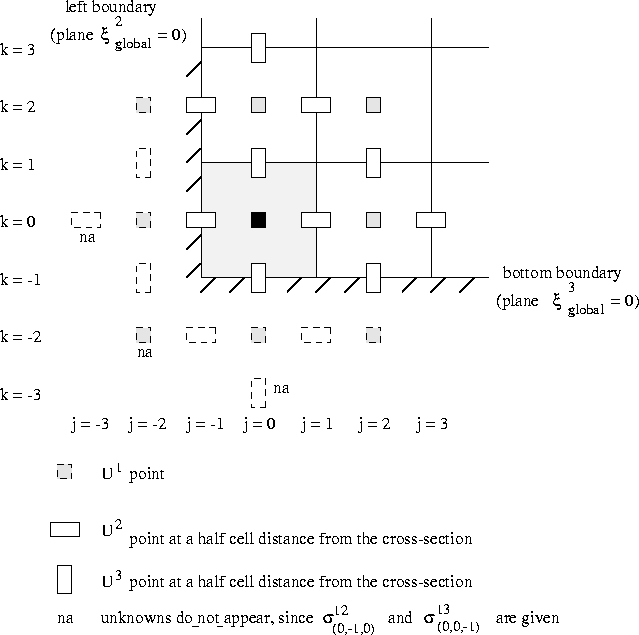
Figure 7.15: Cross-section over the ''tangential'' -cell.
