The boundary conditions for the transport equation are much
easier to implement than the boundary conditions for the velocity
components.
In the case of Dirichlet boundary conditions it is sufficient to use linear
extrapolation to eliminate virtual scalars. So for example in
Figure 7.16 we use the following formulae:
for normal boundary points and
for the corner points.
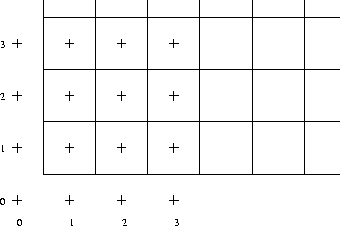
Figure 7.16: Cells for scalar quantities and corresponding virtual points.
In the case of a Robbins boundary condition we follow Van Kan et al. (1991). This means that the Robbins boundary condition
is substituted in the diffusive term:
where 
is the boundary at which the robbins boundary condition
is given. The approximation of the first integral in the right-hand side of
(7.76) is the same as for the inner region. The evaluation of the last
term of the right-hand side of (7.76) on, for example, the left boundary
of the domain is as follows:
In the case of non-smooth grids, the following approximation could be better used:
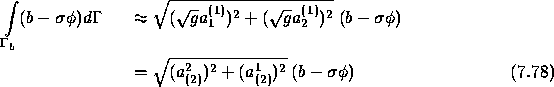
Virtual scalars 
are eliminated in the usual way. Similar expressions may
be found for the three-dimensional case.
