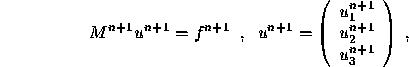
The discretization of the incompressible Navier-Stokes equations in general
curvilinear co-ordinates is described in the foregoing sections. The space
discretization consists of a finite volume technique on a structured grid.
The motivation for these choices is that we want to solve large two and three
dimensional problems. In these problems it is important to obtain fast
iterative methods to solve the discretized equations. This is easier using
a finite volume technique instead of a finite element technique. Finally
the structured grid enables us to develop a good implementation of the
methods on vector computers.
The linear systems to be solved are [36, 37]:
the momentum equations
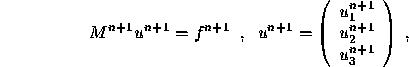
the pressure equation
and eventually one or more transport equations:
transport equations
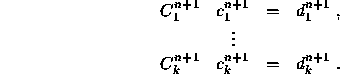
Suppose 
is the number of grid points in the 
-direction,
where we take 
for a 2-dimensional problem. The pressure and
transport matrices have 
rows and columns.
The dimension of the momentum matrix is 
in
2-dimensional problems and 
in
3-dimensional problems.
For the structure of the matrices in 2-dimensions we refer to Vuik (1992)
and Vuik (1993). In the 3-dimensional case the nonzero structure is
symmetric for all matrices. In 3 dimensions the structure of the pressure
equation is given in Figure 10.1.
Note that the nonzero structure is symmetric. The momentum matrix can be
partitioned in the following form:
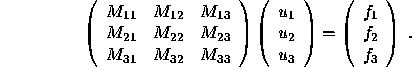
The structure of 
is the same as for the pressure
equations. The off-diagonal blocks contain 16 non zero diagonals. The
non zero structure of the momentum matrix is non symmetric. To illustrate
this we give 
and 
in Figures 10.2 and 10.3
and note the non zero structure of is not equal to the non zero
structure of 
.
In the following table we summarize the number of non zero elements in some
matrices.
Table 10.1: Number of non zero elements
Figure 10.1: The pressure matrix P
In three dimensions the momentum matrix is much larger than the pressure
matrix. The ratio in 2D is equal to 
whereas the
ration in 3D is equal to 
.
So in 3D a momentum matrix times vector is 8 times as expensive as a
pressure matrix times vector.
The momentum matrix and the transport matrix depend on the time t. In
many problems the pressure matrix is independent of the time. However, this
property of the pressure matrix is not used in the current implementation.
Figure 10.3: The momentum-matrix
