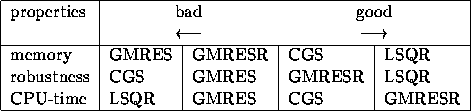
Table 10.2: Properties of the iterative methods
The systems given in Section 10.1 are solved with iterative
methods of CG-type. All the methods used in ISNaS can be applied to
unsymmetric matrices. The methods used in ISNaS are:
This is a stable implementation of CG applied to the normal equations
[20].
CGS is an iterative method based on the Bi-Lanczos algorithm
[27].
An iterative method, which computes an approximation with a minimal
residual [22].
A method based on GMRES, but in general cheaper with respect to work and
memory [33]. In Table 10.2 we summarize the properties of
the iterative methods.
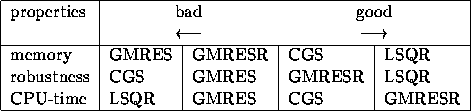
Table 10.2: Properties of the iterative methods
This table only gives an indication of the properties. So in many
experiments the results agree with Table 10.2. However, for specific
problems the results may be different.
For iterative methods it is necessary to specify a stopping criterion. In
general the norm of the residual: ![]() is
easy to obtain. So all our stopping criteria are based on
is
easy to obtain. So all our stopping criteria are based on ![]() .
For the different equations we recommend different stopping criteria. For
the details we refer to Vuik (1992), p. 8 for the momentum equations,
Vuik (1992), p.13 for the pressure equation, and Vuik (1992), p. 15 for a
transport equation.
.
For the different equations we recommend different stopping criteria. For
the details we refer to Vuik (1992), p. 8 for the momentum equations,
Vuik (1992), p.13 for the pressure equation, and Vuik (1992), p. 15 for a
transport equation.
Finally we have to choose a starting vector for the iterative methods.
Since we solve the systems for every timestep, the solution of the
foregoing timestep is in general a good starting vector. For the details we
refer to Vuik (1992), p. 6, 7 for the momentum equations, Vuik (1992), p.
13 for the pressure equation, and Vuik (1992), p. 15 for a transport
equation.