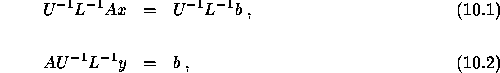
In many applications, iterative methods are combined with a preconditioner [17]. It is a well known fact that a good preconditioner is very important in order to obtain fast iterative methods. The preconditioners used in ISNaS are based on incomplete LU decompositions. In such a preconditioner, one constructs a lower triangular matrix L and an upper triangular matrix U, where L and U have a prescribed nonzero pattern, and LU is a good approximation of A. The iterative methods can be applied to
or
We call equation (10.1) a preconditioned system and equation
(10.2) a postconditioned system. The final equation is only used in
combination with the Eisenstat implementation [5]. In general, the
convergence behaviour of a Krylov type iterative method depends on the
eigenvalue distribution of the matrix. In the three equations given above
the eigenvalues of the product-matrices are the same. So the convergence
behaviour is approximately the same when we use (10.1), (10.2), or (10.3). A small
advantage of a postconditioned system is that the norm of a residual is not
influenced by the matrices L and U (compare [36], p. 12,
13).
Below we give a short description of the preconditioners used in ISNaS.
A diagonal preconditioner is obtained by choosing L = I and 
. This is a cheap preconditioner with respect to memory and can be used
in combination with vector and parallel computers. For most problems the
gain in the number of iterations is small.
For this preconditioner we construct 
as an approximation of
A. To obtain L, D, and U we use the following rules [32]:
The third rule can be replaced by the following:
;
.
which leads to the MILU preconditioning. We always use an average of ILUD
and MILUD. This preconditioner is also cheap with respect to memory. It
costs two extra vectors, one for D and the other one for
. Using the
Eisenstat implementation we are able to save one matrix vector product per
iteration. In the ISNaS program ILUD preconditioner means application of
the iterative method to (10.3) and not to (10.1), which is
done in the other preconditioners. Multiplication with 
and
leads to recurrencies. So these parts do not run in vector speed
on a vector computer.
This preconditioner is only used for the pressure and transport equations.
The matrices L and U are constructed such that LU approximates A
and satisfies the following rules:
Again the last rule for i = j can be repaced by
;
then 
.
which leads to MILU. We always use an average of ILU and MILU. The
convergence behaviour of an iterative method combined with MILU is in
general beter than a combination with MILUD. A disadvantage is that extra
memory space is needed to store L and U. The amount of extra memory is
the same as the amount of memory to store A. Furthermore it is impossible
to save a matrix vector product per iteration (compare the Eisenstat
implementation). From our experiments we conclude that if the memory space
is available than it is better to use MILU.
During the solution of the pressure or transport equation the memory space
of the momentum matrix is available. For this reason we always use the MILU
preconditioner to solve the pressure and transport equations, and the MILUD
preconditioner for the momentum equations.
Due to the recurrencies, the multiplication of or for MILUD or
MILU runs in scalar speed on a vector computer. In the ISNaS program the
loops are rewritten in such a way that they run in vectorspeed
[1]. Note that
the rewritten loops use indirect adressing and are much shorter than the
original loops. On the Convex C3840 this leads to good results.
