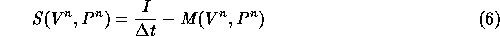
The pressure correction algorithm (3)--(5) is used for Navier-Stokes solution on the global domain. The equations (3) and (4) are solved using domain decomposition. In this paper, we assume that the subdomains intersect regularly, that is the grid lines are continuous across block-interfaces. For the description of the domain decomposition algorithm, we start from a discretization of the momentum and pressure equations on the global grid.
The discretization matrix of the linearized momentum equations on the global domain is
and the discretization matrix of the pressure equations on the global domain is
with D the global divergence and G the global gradient operator.
Equations (6) and (7) are solved
using domain decomposition. The correction of 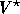 is carried
out in all blocks independently.
is carried
out in all blocks independently.
Both the pressure equations (4) and the momentum equations (3) can be written as
with either A = S from (6) and v = V for the
momentum equations or A = T from (7) and 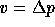 for the pressure equations.
If we decompose A into blocks such that each block corresponds to
all unknowns in a single subdomain, with a small modification for
the momentum equations, see further on, then for two subdomains
for the pressure equations.
If we decompose A into blocks such that each block corresponds to
all unknowns in a single subdomain, with a small modification for
the momentum equations, see further on, then for two subdomains
where 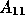 and
and  represent the subdomain discretization
matrices and
represent the subdomain discretization
matrices and 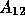 and
and 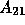 represent the coupling between
subdomains.
Unaccelerated domain decomposition iteration for (8)
is of the following form
represent the coupling between
subdomains.
Unaccelerated domain decomposition iteration for (8)
is of the following form
with
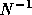 an approximation to the inverse of the block diagonal or
block lower-triangular matrix of A. The matrix N is called the
block Jacobi or Gauss-Seidel matrix of A, depending on the method used.
an approximation to the inverse of the block diagonal or
block lower-triangular matrix of A. The matrix N is called the
block Jacobi or Gauss-Seidel matrix of A, depending on the method used.
Block Gauss-Seidel and Jacobi iterations are algebraic generalizations of the Schwarz domain decomposition algorithm [42,34]. Similar to Schwarz domain decomposition, in each iteration, subdomain problems are solved using values from neighboring blocks. For instance, formula (10) interpreted for domain 1 becomes
where
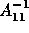 represents subdomain solution and
represents subdomain solution and 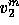 are the values
from the neighboring block.
The subdomain problems,
are the values
from the neighboring block.
The subdomain problems, 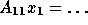 and
and 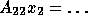 are solved using GMRES [41] with appropriate
preconditioners [50].
GMRES may be used to solve subdomain problems as well as to accelerate
domain decomposition.
We cannot apply the above described block Gauss-Seidel
and Jacobi algorithms directly to the momentum matrix S
because the normal velocity components at the block interfaces belong to two blocks.
First we augment the matrix S in the following way.
For the sake of argument, consider a decomposition into two blocks as in
Figure 3.
are solved using GMRES [41] with appropriate
preconditioners [50].
GMRES may be used to solve subdomain problems as well as to accelerate
domain decomposition.
We cannot apply the above described block Gauss-Seidel
and Jacobi algorithms directly to the momentum matrix S
because the normal velocity components at the block interfaces belong to two blocks.
First we augment the matrix S in the following way.
For the sake of argument, consider a decomposition into two blocks as in
Figure 3.
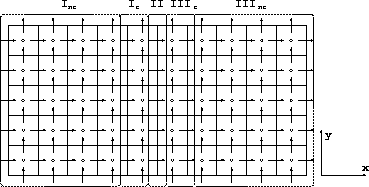
Figure 3: Definition of three sets of unknowns. 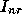 and
and 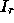 consistute set
I and
consistute set
I and 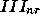 and
and 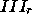 consitute set III
consitute set III
Suppose that the velocity unknowns are divided into 3 sets as in Figure 3.
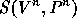 has
the block form:
has
the block form:
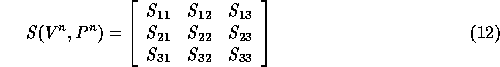
The system of equations 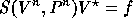 can be transformed
to the equivalent system
can be transformed
to the equivalent system
The solution of (13) always satisfies
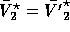 if
if 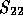 is invertible
(see [45]) and therefore the system (13) is equivalent
to the original system of equations
is invertible
(see [45]) and therefore the system (13) is equivalent
to the original system of equations 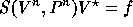 .
In view of (9), we have
.
In view of (9), we have
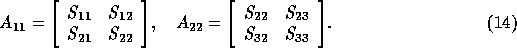
so that domain decomposition for the momentum equations has been described.
In (11), 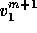 only depends on
only depends on 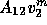 .
Since
.
Since 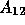 only has non-zero coefficients for unknowns in
only has non-zero coefficients for unknowns in
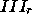 , see Figures 2 and 3,
the left-hand side
, see Figures 2 and 3,
the left-hand side 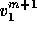 only depends on these components.
Analogously,
only depends on these components.
Analogously, 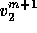 only depends on the components of
only depends on the components of 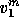 in region
in region 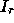 . The components in
. The components in 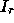 and
and 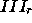 are assembled
in a vector
are assembled
in a vector 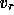 also called the interface unknowns,
and the remaining ones in
also called the interface unknowns,
and the remaining ones in 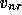 .
The normal fluxes at the block interface in region II are a part of the
inner regions of the subdomains, and are solved for in each iteration.
.
The normal fluxes at the block interface in region II are a part of the
inner regions of the subdomains, and are solved for in each iteration.
Finally, the last step (5) of the pressure-correction algorithm is carried out in all blocks independently. The above discussion can be easily extended to the general multi-domain case. Also extensions to irregular intersections are possible, see for example [2,30,53].