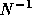In [11] subdomain problems are assumed to be
solved accurately so that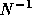 
is the exact inverse of the
block diagonal or block lower-triangular matrix of A, so
with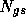 
the Gauss-Seidel version and
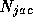the Jacobi version of N.
The Gauss-Seidel version is suitable for implementation on a single
processor and leads to the sequential or multiplicative algorithm.
The Jacobi version is suitable for parallelization and is called
the parallel or additive version.
It can be
seen from Figure 2 and 3
that the left-hand side of (10) only depends on the
values of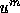 
in regions 
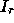and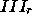 
in Figure 3.
The unknowns u are ordered in such a way that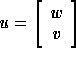 
,
where v are the interface
unknowns (regions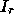 
, 
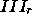), and w are remaining unknowns.
We have
with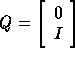 
an injection operator such that
.
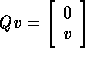By substituting (16) into (10) and by premultiplying with
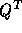we get
Since we are interested in the stationary solution v of (17) we get
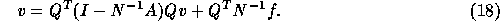
which is equivalent to
In this way, accurate solution of subdomain problems finally leads to a system involving only the interface equations. Accelerated domain decomposition in [11] amounts to solving the interface equations (19) using GMRESR [46]. In the present paper, we use GMRES: the required matrix-vector product can be computed by doing one domain decomposition iteration, see [11] for details.
