The turbulence model equations, as discussed in the previous section, are
transport equations. Hence, for the implementation of the two-equation models the
equation (5.2) will be considered. The evaluation of the functions 
,
, D and 
for each turbulence equations must result
in a positive scheme, which means that the solution of turbulence quantities
assumes non-negative. This positivity consideration is urged because of our
desire to develop efficient and robust method for turbulent transport equations.
See also [42].
It should be mentioned that in case of space discretization the positivity of
the turbulence quantities is guaranteed via TVD constraints on the
convection scheme, as has been discussed in Section 5.3.
The turbulence source term has a considerable impact on the time integration. It
turns out that we are compelled to use standard Newton linearization in order to
avoid the possibility of negative solution of turbulence quantities. As an
example, we consider the equation for turbulent kinetic energy in the
high-Reynolds-number standard k- 
model where the source term is
with 
. The treatment of the quadratic
term in the production rate of turbulent energy, due to the use of an anisotropy
model, will be discussed later. The eddy-viscosity and consequently the production
term will be frozen at time level n, whereas the dissipation term will be
treated implicitly and linearized as follows:
where n denotes the preceding time level and n+1 the new time level.
The functions D and becomes
The other functions are given by
The same holds for the equation for dissipation rate. We have
An analogous procedure is followed in respect of the k- 
model.
So far, we have considered the standard k- model. The extra term
in the RNG dissipation rate equation should also be treated appropriately.
Consider the term
then by replacing the functions D and , respectively, with
and 
, it can be verified that the
right-hand side of the discrete equation for and the coefficient of
consist of positive contributions.
Physically, the production rate of turbulent energy is always non-negative. The
problem, however, is that, when employing an anisotropic model, there is no
guarantee that 
is non-negative numerically. Hence, special measures are
taken to ensure that at no stage of the time stepping the production rate assume
negative values. By virtue of (6.9), (6.3) and (6.27) one
sees that
The first term in the right-hand side of (6.58) is always non-negative and
hence, can be contributed to , as explained before. The second term would
normally be expected to contribute to . However, it must only do so if it is
non-negative, otherwise it must be allocated to D. This can be done in the
following way: this negative term is first divided by the value of k available
from the previous time level and then added to D. Algebraically, this is
implemented through,
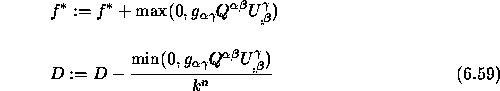
An analogous procedure is followed in respect of the dissipation rate equation.
