Machine Learning
Aritificial intelligence (AI) and machine learning (ML) have seen a leap forward in popularity in the last years. Our research in this field mainly focusses on scientific maschine learning, where we combine deep-learning techniques with classical numerical methods such as Isogeometric Analysis.
The figure below shows two solutions to the two-dimensional Poisson equation predicted by a deep neural network. Following the IGA paradigm, geometry, boundary conditions, and the solution are represented in terms of B-spline bases. The network inputs/outputs are the respective coefficients, which makes the evaluation of the trained network for changing problem instances straightforward.
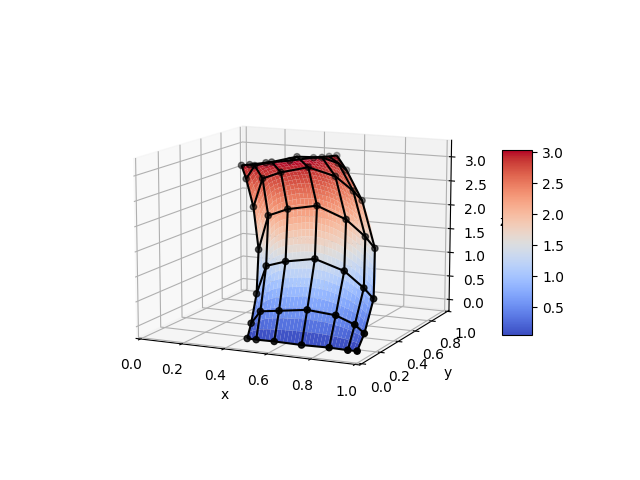
Credits: Frank van Ruiten, 2020
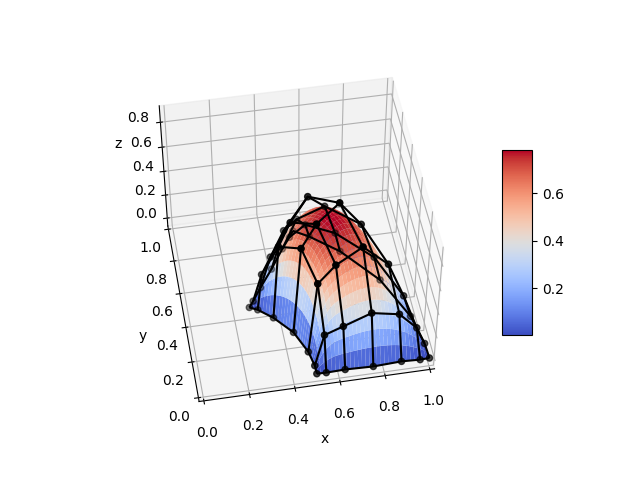
We modified the above approach to design free-form optics that generate a specific target light distribution.
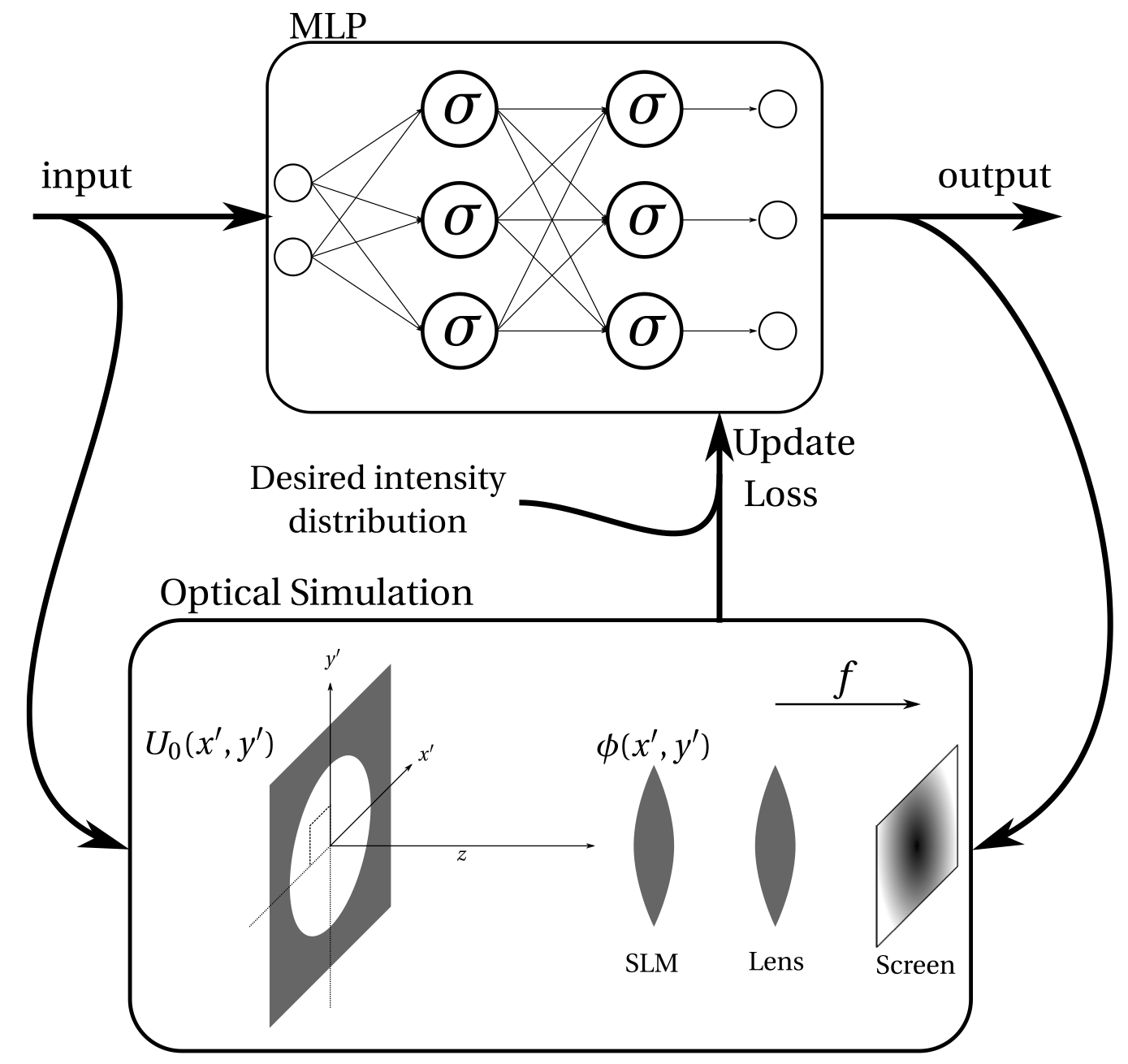
Credits: Lucas Crijns, 2021
Selected contributions
- Bart de Koning, Alexander Heemels, Aurele Adam, and Matthias Möller. Gradient descent-based freeform optics design for illumination using algorithmic differentiable non-sequential ray tracing. Optimization and Engineering, September 2023. [ DOI | http ]
- Dylan Everingham. Topology optimization and physics-informed neural networks for metamaterial optics design, 2022. [ http ]
- Samarth Kakkar. Physics-informed deep learning for computational fluid flow analysis: Coupling of physics-informed neural networks and autoencoders for aerodynamic flow predictions on variable geometries, 2022. [ http ]
- Bart de Koning. Designing free-form optics for multiple-source illumination using differentiable ray-tracing and neural networks, 2022. [ http ]
- Marek Oerlemans. Diffractive optical elements are all you need: Designing an optical system using physics-informed and data-driven methods, 2022. [ http ]
- Frank van Ruiten. PINNs for parametrized problems, 2022. [ http ]
- Rana Sannia Ul Haq. Stabilizing convection-dominated flow problems using neural networks based on flux-limiting techniques, 2022. [ http ]
- Lucas Crijns. PINN inspired freeform design: Using Fraunhofer diffraction to find freeforms described by B-spline surfaces, 2021. [ http ]
- Fernando Wanguemert Guerra. Physics informed neural networks, a new approach for the solution of PDEs, 2021. [ http ]
- Matthias Möller, Deepesh Toshniwal, and Frank van Ruiten. Physics-informed machine learning embedded into isogeometric analysis. In Mathematics: Key enabling technology for scientific machine learning. Platform Wiskunde, 2021. [ http ]
- Merel Schalkers. Learning based hardware-centric quantum circuit generation, 2021. [ http ]
- Jort Bouma. Using a physics-informed neural network to solve the ideal magnetohydrodynamic equations, 2020. [ http ]
- Joost Imhoff. Freeform lens predictions by a neural network and B-splines, 2020.
- Susan Veldkamp. Het ontbinden van een matrix m.b.v. een getraind neuraal netwerk, 2020. [ http ]
- Franziska Riegger. Image segmentation of the γ'-phase in nickelbase superalloys utilising deep learning, 2019. [ http ]